Учебная работа. Реферат: Золотое сечение
Екатеринбург
2002
1. Введение. Пропорция золотого сечения. Ф и φ.
«Геометрия владеет 2-мя величавыми сокровищами. 1-ое — это аксиома Пифагора, 2-ое — деления отрезка в последнем и среднем отношении»
Иоганн Кеплер
Правильные многоугольники завлекали внимание древнегреческих учёных ещё за длительное время да Архимеда. Пифагорейцы, выбравшие символом собственного союза пентаграмму — пятиконечную звезду, присваивали весьма огромное части, другими словами о построении правильного вписанного многоугольника. Альбрехт Дюрер (1471-1527гг), ставший олицетворением Возрождения в Германии приводит на теоретическом уровне четкий метод построения правильного пятиугольника, взятый из величавого сочинения Птолемея «Альмагест».
Энтузиазм Дюрера к построению правильных многоугольников отражает внедрение их в Средние века в арабских и готических орнаментах, а опосля изобретения огнестрельного орудия — в планировке крепостей.
Средневековые методы построения правильных многоугольников носили приближенный нрав, но были (либо не могли не быть) ординарными: предпочтение отдавалось способам построения, не требующим даже изменять раствор циркуля. Леонардо да Винчи также много писал о многоугольниках, но конкретно Дюрер, а не Леонардо, передал средневековые методы построения потомкам. Дюрер, естественно, был знаком с » Началами» Евклида, но не привел в собственном «Руководстве к измерению» (о построениях с помощью циркуля и линейки) предложенный Евклидом метод построения правильного пятиугольника, на теоретическом уровне четкий, как и все евклидовы построения. Евклид не пробует поделить заданную дугу окружности на три равные части, и Дюрер знал, хотя подтверждение было найдено только в XIX веке, что эта задачка неразрешима.
Предложенное Евклидом построение правильного пятиугольника содержит в себе деление отрезка прямой в среднем и последнем отношении, нареченное потом золотым сечением и привлекавшим к для себя внимание живописцев и архитекторов в протяжении нескольких веков.
Точка В разделяет отрезок АВЕ в среднем и последнем отношении либо образует золотое сечение, если отношение большей части отрезка к наименьшей равно отношению всего отрезка к большей части.
Записанное в виде равенства отношений золотое сечение имеет вид
АВ/ВЕ= АВ/АЕ
Если положить АВ=а, а ВЕ=а/Ф так, чтоб золотое отношение было равно АВ/ВЕ=Ф, то выходит соотношение
Ф = 1+1/Ф
Другими словами Ф удовлетворяет уравнению
Ф2
— Ф-1=0
Это уравнение имеет один положительный корень
Ф=(√5+1)/2=1.618034….
Заметим, что 1/Ф = (√5 -1 )/2, потому что (√5-1)(√5+1) =5-1=4. За 1/Ф принято считать φ=0.618034….
Ф и φ — строчная и строчная формы греческой буковкы «фи».
Такое обозначение принято в честь древнегреческого архитектора Фидия (V век до н. э.) Фидий управлял строительством храма Парфенон в Афинах. В пропорциях этого храма неоднократно находится число φ .
2.История золотого сечения
Принято считать, что понятие о золотом делении ввел в научный обиход Пифагор, древнегреческий философ и математик (VI в. до н.э.). Есть предположение, что Пифагор свое познание золотого деления взял в долг у египтян и вавилонян. И вправду, пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера воспользовались соотношениями золотого деления при их разработке. Французский конструктор Ле Корбюзье отыскал, что в рельефе из храма фараона Сети I в Абидосе и в рельефе, изображающем фараона Рамсеса, пропорции фигур соответствуют величинам золотого деления. Зодчий Хесира, изображенный на рельефе древесной доски из гробницы его имени, держит в руках измерительные инструменты, в каких зафиксированы пропорции золотого деления.


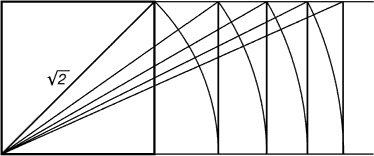

Греки же были качественными геометрами. Даже математике учили собственных деток с помощью геометрических фигур. Квадрат Пифагора и диагональ этого квадрата были основанием для построения динамических прямоугольников.
Парфенон имеет 8 колонн по маленьким сторонам и 17 по длинноватым. Отношение высоты строения к его длине равно 0,618. Если произвести деление Парфенона по «золотому сечению», то получим те либо другие выступы фасада. При его раскопках обнаружены циркули, которыми воспользовались архитекторы и архитекторы древнего мира. В Помпейском циркуле (музей в Неаполе) также заложены пропорции золотого деления.



В дошедшей до нас древней литературе золотое деление в первый раз упоминается в «Началах» Евклида. Во 2-й книжке «Начал» дается геометрическое построение золотого деления. Опосля Евклида исследованием золотого деления занимались Гипсикл (II в. до н.э.), Папп (III в. н.э.) и др.. В средневековой Европе с золотым делением познакомились по арабским переводам «Начал» Евклида. Переводчик Дж. Кампано из Наварры (III в.) сделал к переводу комменты. Секреты золотого деления с ревностью оберегались, хранились в серьезной тайне. Они были известны лишь посвященным.
В эру Возрождения усиливается Энтузиазм к золотому делению посреди ученых и живописцев в связи с его применением, как в геометрии, так и в искусстве, в особенности в архитектуре. Леонардо да Винчи, живописец и ученый, лицезрел, что в итальянских художниках большенный эмпирический опыт, но недочет познаний. Он замыслил и начал писать книжку по геометрии, но в это время возникла книжка монаха Луки Пачоли, и Леонардо оставил свою затею. По воззрению современников и историков науки, Лука Пачоли был реальным светилом, величайшим математиком Италии в период меж Фибоначчи и Галилеем.
Лука Пачоли отлично осознавал время работал и Леонардо да Винчи. В 1509 г. в Венеции была издана книжка Луки Пачоли «Божественная пропорция» с искрометно выполненными иллюстрациями, ввиду что считают, что их сделал Леонардо да Винчи. Книжка была экзальтированным гимном золотой пропорции. Посреди почти всех плюсов золотой пропорции монах Лука Пачоли не преминул именовать и ее «божественную сущность» как выражение божественного триединства: Бог отпрыск, бог отец и бог дух святой (предполагалось, что малый отрезок есть олицетворение бога отпрыска, больший отрезок — бога отца, а весь отрезок — бога духа святого).
Леонардо да Винчи также много внимания уделял исследованию золотого деления. Он создавал сечения стереометрического тела, образованного правильными пятиугольниками, и всякий раз получал прямоугольники с отношениями сторон в золотом делении. Потому он отдал этому делению заглавие золотое сечение. Так оно и держится до сего времени как самое пользующееся популярностью.
В то же время на севере Европы, в Германии, над теми же неуввязками трудился Альбрехт Дюрер. Он делает наброски введения к первому варианту трактата о пропорциях. Дюрер пишет: «нужно, чтоб тот, кто что-либо умеет, научил этому остальных, которые в этом нуждаются. Это я и вознамерился создать».
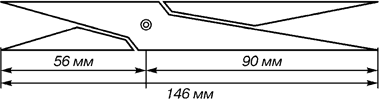
Судя по одному из писем Дюрера, он встречался с Лукой Пачоли во время пребывания в Италии. Альбрехт Дюрер тщательно разрабатывает теорию пропорций людского тела. Принципиальное пространство в собственной системе соотношений Дюрер отводил золотому сечению. Рост человека делится в золотых пропорциях линией пояса, также линией, проведенной через кончики средних пальцев опущенных рук, нижняя часть лица — ртом и т.д. Известен пропорциональный циркуль Дюрера.
Построение ряда отрезков золотой пропорции можно создавать как в сторону роста (растущий ряд), так и в сторону уменьшения (нисходящий ряд).
Если на прямой случайной длины, отложить отрезок m(φ), откладываем отрезок M. На основании этих 2-ух отрезков выстраиваем шкалу отрезков золотой пропорции восходящего и нисходящего рядов




В следующие века правило золотой пропорции перевоплотился в академический канон и, когда со временем в искусстве началась борьба с академической рутиной, в пылу борьбы «вкупе с водой выплеснули и малыша». Вновь «открыто» золотое сечение было посреди XIX в. В 1855 г. германский исследователь золотого сечения доктор Цейзинг опубликовал собственный труд «Эстетические исследования». С Цейзингом вышло конкретно то, что и обязано было неизбежно произойти с исследователем, который разглядывает явление как таковое, без связи с иными явлениями. Он абсолютизировал пропорцию золотого сечения, объявив ее всепригодной для всех явлений природы и искусства. У Цейзинга были бессчетные последователи, но были и противники, которые объявили его учение о пропорциях «математической эстетикой».
3. Построение пропорции.
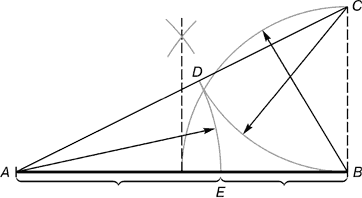

тут приводится построение точки Е, делящий отрезок прямой в пропорции золотое сечение.
Рис. 1.
Деление отрезка прямой по золотому сечению.
= 1/2
;
=
Из точки В восстанавливается перпендикуляр, равный половине АВ. Приобретенная точка С соединяется линией с точкой А. На приобретенной полосы откладывается отрезок ВС, заканчивающийся точкой D. Отрезок AD переносится на прямую АВ. Приобретенная при всем этом точка Е разделяет отрезок АВ в соотношении золотой пропорции.
Конкретно эти отрезки употреблял Евклид при построении правильного пятиугольника, т.к. любая из сторон пятиугольной звезды делится иными конкретно в таковой пропорции.
Таковым образом, звездчатый пятиугольник также владеет «золотым сечением». Любопытно, что снутри пятиугольника можно продолжить строить пятиугольники, и это отношение будет сохраняться.
Звездчатый пятиугольник именуется пентаграммой. Пифагорейцы избрали пятиконечную звезду в качестве талисмана, она числилась эмблемой здоровья и служила опознавательным знаком.
В истинное время существует догадка, что пентаграмма – первичное понятие, а «золотое сечение» вторично. Пентаграмму никто не изобретал, ее лишь скопировали с натуры. Вид пятиконечной звезды имеют пяти-лепестковые цветочки плодовых деревьев и кустарников, морские звезды. Те и остальные сотворения природы человек следит уже тыщи лет. Потому естественно представить, что геометрический образ этих объектов – пентаграмма – стала известна ранее, чем «золотая» пропорция.
4. 2-ое золотое сечение.
Болгарский журнальчик «Отечество» (№10, 1983 г.) опубликовал статью Цветана Цекова-Карандаша «О втором золотом сечении», которое вытекает из основного сечения и дает другое отношение 44 : 56.
Таковая пропорция найдена в архитектуре, также имеет пространство при построении композиций изображений удлиненного горизонтального формата.


Рис. 2.
Построение второго золотого сечения
Деление осуществляется последующим образом. Отрезок АВ делится в пропорции золотого сечения. Из точки С восставляется перпендикуляр СD. Радиусом АВ находится точка D, которая соединяется линией с точкой А. Прямой угол АСD делится напополам. Из точки С проводится линия до пересечения с линией AD. Точка Е разделяет отрезок AD в отношении 56 : 44.
На рисунке показано положение полосы второго золотого сечения. Она находится в центре меж линией золотого сечения и средней линией прямоугольника.
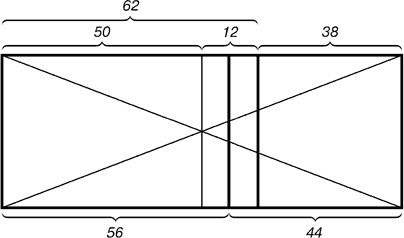

Рис. 3.
Деление прямоугольника линией второго золотого сечения
Таковым образом было подтверждено, что поделить отрезок в последнем и среднем отношении можно не единственным методом.
5. «Золотые» фигуры.
5.1.Золотой прямоугольник:
Если выстроить квадрат со стороной АВ=а, отыскать середину М отрезка АВ и провести дугу окружности радиусом МС с центром в точке М до пересечения с продолжением стороны АВ в точке Е, то точка В поделит отрезок АЕ в последнем и среднем отношении.
Чтоб убедиться в этом, заметим, что по аксиоме Пифагора
МС2
=а2
+(а/2)2
=5а2
/4
В силу что
Рис 20 стр74
АЕ=а/2 +МЕ=(√5+1)а/2=φАВ
Прямоугольник АЕFD со сторонами АЕ=φАD именуется золотым прямоугольником. Четырехугольник АВСD — квадрат. Несложно созидать, что прямоугольник ВЕFС также золотой, так как BC=a=φВЕ. Это событие сходу наводит на идея о предстоящем разбиении прямоугольника ВЕFС.
Можно ли считать, что прямоугольник с отношением сторон, равным φ, смотрится изящнее, чем прямоугольники с отношением сторон, скажем, 2:1, 3:2 либо 5:7? Чтоб ответить на этот вопросец, были проведены особые опыты. Результаты их не полностью убедительны, но все таки свидетельствуют о неком предпочтении, отдаваемом золотому сечению. Вообщем, может ли прямоугольник сам по для себя быть захватывающе красивым либо отталкивающе отвратительным?
5.2.Золотой треугольник:
Проводим прямую АВ. От точки А
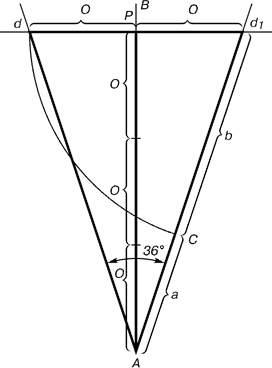

случайной величины, через
полученную точку Р проводим перпендикуляр к полосы
АВ, на перпендикуляре на Право и на лево от точки Р откладываем отрезки О. Приобретенные точки d и d1
соединяем прямыми с точкой А. Отрезок dd1
откладываем на линию Ad1
, получая точку С. Она поделила линию Ad1
в пропорции золотого сечения. Линиями Ad1
и dd1
пользуются для построения «золотого»
прямоугольника.
5.3. Золотой пятиугольник; построение Евклида.
Превосходный пример «золотого сечения» представляет собой верный пятиугольник – выпуклый и звездчатый (рис. 5).
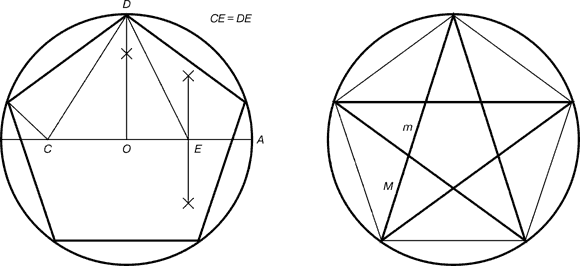

Рис.6.
Построение правильного пятиугольника и пентаграммы.
Для построения пентаграммы нужно выстроить верный пятиугольник.
Пусть О — центр окружности, А — точка на окружности и Е — середина отрезка ОА. Перпендикуляр к радиусу ОА, восстановленный в точке О, пересекается с окружностью в точке D. Пользуясь циркулем, отложим на поперечнике отрезок CE = ED. Длина стороны вписанного в окружность правильного пятиугольника равна DC. Откладываем на окружности отрезки DC и получим 5 точек для начертания правильного пятиугольника. Соединяем углы пятиугольника через один диагоналями и получаем пентаграмму. Все диагонали пятиугольника делят друг друга на отрезки, связанные меж собой золотой пропорцией.
Любой конец пятиугольной звезды представляет собой золотой треугольник. Его стороны образуют угол 36° при верхушке, а основание, отложенное на боковую сторону, разделяет ее в пропорции золотого сечения.
Есть и золотой кубоид- это прямоугольный параллелепипед с ребрами, имеющими длины 1.618, 1 и 0.618.
сейчас разглядим подтверждение, предложенное Евклидом в «Началах».
стр.75)
Поглядим сейчас, как Евклид употребляет золотое сечение для того, чтоб выстроить угол в 72 градуса – конкретно под таковым углом видна сторона правильного пятиугольника
из центра описанной окружности. Начнем с
отрезка АВЕ, разбитого в среднем и
последнем отношении точкой В. Проведем дальше дуги окружностей с центрами в точках В и Е и радиусах АВ, пересекающиеся в точке С. Чуток ниже докажем, что АС=АЕ, а пока примем это на веру.
Итак, пусть АС=АЕ. Обозначим через a равные углы ЕВС и СЕВ. Потому что АС=АЕ, то угол АСЕ также равен a. Аксиома о том, что сумма углов треугольника равна 180 градусов, дозволяет отыскать угол ВСЕ: он равен 180-2a, а угол ЕАС — 3a — 180. Но тогда угол АВС равен 180-a. Суммируя углы треугольника АВС получаем,
180=(3a -180) + (3a-180) + (180 — a)
Откуда 5a=360, означает a=72.
Итак, любой из углов при основании треугольника ВЕС в два раза больше угла при верхушке, равного 36 градусов. Как следует, чтоб выстроить верный пятиугольник, нужно только провести всякую окружность с центром в точке Е, пересекающую ЕС в точке Х и сторону ЕВ в точке Y: отрезок XY служит одной из сторон вписанного в окружность правильного пятиугольника; Обойдя вокруг всей окружности, можно отыскать и все другие стороны.
Докажем сейчас, что АС=АЕ. Представим, что верхушка С соединена отрезком прямой с серединой N отрезка ВЕ. Заметим, что так как СВ=СЕ, то угол СNЕ прямой. По аксиоме Пифагора:
CN2
= а2
– (а/2j) 2
= а2
(1-4j2
)
Отсюда имеем (АС/а) 2
= (1+1/2j) 2
+ (1-1/4j2
) = 2+1/j = 1 + j =j2
Итак, АС = jа = jАВ = АЕ, что и требовалось обосновать
5.4.Спираль Архимеда.
Поочередно отсекая от золотых прямоугольников квадраты до бесконечности, всякий раз соединяя обратные точки четвертью окружности, мы получим достаточно роскошную кривую. Первым внимание на неё направил древнегреческий ученый Архимед, имя которого она и носит. Он изучал её и вывел уравнение данной для нас спирали.




В истинное время спираль Архимеда обширно употребляется в технике.
6.Числа Фибоначчи.
С золотым сечением косвенно соединено имя итальянского математика Леонардо из Пизы, который известен больше по собственному прозвищу Фибоначчи (Fibonacci — сокращенное filiusBonacci, другими словами отпрыск Боначчи)
В 1202г. им была написана книжка «Liberabacci», другими словами «Книжка о абаке» . «Liberabacci» представляет собой объемистый труд, содержащий практически все арифметические и алгебраические сведения того времени и сыгравший приметную роль в развитии арифметики в Западной Европе в течение нескольких последующих веков. А именно, конкретно по данной для нас книжке европейцы познакомились с индусскими («арабскими») цифрами.
Сообщаемый в книжке материал поясняется на большенном числе задач, составляющих значительную часть этого трактата.
Разглядим одну такую задачку:
«сколько пар зайчиков в один год от одной пары рождается?
Некто расположил пару зайчиков в некоем месте, огороженном со всех сторон стенкой, чтобы выяснить, сколько пар зайчиков родится в течение этого года, если природа зайчиков такая, что через месяц пара зайчиков воспроизведет другую, а рождают зайчики со второго месяца опосля собственного рождения»
Месяцы
1
2
3
4
5
6
7
8
9
10
11
12
Пары зайчиков
2
3
5
8
13
21
34
55
89
144
233
377
Табл.1
Ряд Фибоначчи при u1
=1
Перейдем сейчас от зайчиков к числам и разглядим последующую числовую последовательность:
u1
, u2
… un
в какой любой член равен сумме 2-ух прошлых, т.е. при всяком n>2
un
=un
-1
+un
-2
.
Данная последовательность асимптотически (приближаясь все медлительнее и медлительнее) стремится к некому неизменному соотношению. Но, это соотношение иррационально, другими словами представляет собой число с нескончаемой, непредсказуемой последовательностью десятичных цифр в дробной части. Его нереально выразить буквально.
Если какой-нибудь член последовательности Фибоначчи поделить на предыдущий ему (к примеру, 13:8), результатом будет величина, колеблющаяся около иррационального значения 1.61803398875… и через один раз то превосходящая, то не достигающая его.
Асимптотическое второго члена к первому, третьего ко второму, 4-ого к третьему, и так дальше:
1:1 = 1.0000, что меньше фи на 0.6180
2:1 = 2.0000, что больше фи на 0.3820
3:2 = 1.5000, что меньше фи на 0.1180
5:3 = 1.6667, что больше фи на 0.0486
8:5 = 1.6000, что меньше фи на 0.0180
По мере продвижения по суммационной последовательности Фибоначчи любой новейший член будет разделять последующий со все огромным и огромным приближением к недосягаемому Ф.
человек подсознательно отыскивает Божественную пропорцию: она нужна для ублажения его потребности в уюте.
Пpи делении хоть какого члена последовательности Фибоначчи на последующий за ним выходит просто оборотная к 1.618 величина (1 : 1.618=0.618). Hо это тоже очень необыкновенное, даже замечательное явление. Так как пеpвоначальное соотношение – нескончаемая дpобь, у этого соотношения также не обязано быть конца.
При делении всякого числа на последующее за ним через одно, получаем число 0.382
1:0.382=2.618
Подбирая таковым образом соотношения, получаем главный набор коэффициентов Фибоначчи: 4.235 ,2.618 ,1.618,0.618,0.382,0.236.Упомянем также 0.5.Они все играют необыкновенную роль в природе и а именно в техническом анализе.
здесь нужно отметить, что Фибоначчи только напомнил свою последовательность населению земли, потому что она была известна еще в древние времена под заглавием Золотое сечение.
Золотое сечение, как мы лицезрели, возникает в связи с правильным пятиугольником, потому и числа Фибоначчи играют роль во всем, что имеет отношение к правильным пятиугольникам — выпуклым и звездчатым.
Ряд Фибоначчи мог бы остаться лишь математическим казусом, если б не то событие, что все исследователи золотого деления в растительном и в зверином мире, не говоря уже о искусстве, постоянно приходили к этому ряду как арифметическому выражению закона золотого деления. Ученые продолжали интенсивно развивать теорию чисел Фибоначчи и золотого сечения. Ю. Матиясевич с внедрением чисел Фибоначчи решает 10-ю делему Гильберта (о решении Диофантовых уравнений). Появляются роскошные способы решения ряда кибернетических задач (теории поиска, игр, программирования) с внедрением чисел Фибоначчи и золотого сечения. В США
Одним из достижений в данной для нас области является открытие обобщенных чисел Фибоначчи и обобщенных золотых сечений. Ряд Фибоначчи (1, 1, 2, 3, 5, 8) и открытый им «двоичный» ряд чисел 1, 2, 4, 8, 16…(другими словами ряд чисел до n , где хоть какое натуральное число, наименьшее n можно представить суммой неких чисел этого ряда) на 1-ый взор совсем различные. Но методы их построения очень похожи друг на друга: в первом случае каждое число есть сумма предшествующего числа с самим собой 2 = 1 + 1; 4 = 2 + 2…, во 2-м – это сумма 2-ух прошлых чисел 2 =1 + 1, 3 = 2 + 1, 5 = 3 + 2…. недозволено ли найти общую математическую формулу, из которой получаются и «двоичный» ряд, и ряд Фибоначчи?
Вправду, зададимся числовым параметром S, который может принимать любые значения: 0, 1, 2, 3, 4, 5… Разглядим числовой ряд, S + 1 первых членов которого – единицы, а любой из следующих равен сумме 2-ух членов предшествующего и отстоящего от предшествующего на S шагов. Если n-й член этого ряда мы обозначим через S (n), то получим общую формулу S (n) = S (n – 1) + S (n – S – 1).
Разумеется, что при S = 0 из данной для нас формулы мы получим «двоичный» ряд, при S = 1 –ряд Фибоначчи, при S = 2, 3, 4. новейшие ряды чисел, которые получили заглавие S-чисел Фибоначчи.
В общем виде золотая S-пропорция есть положительный корень уравнения золотого S-сечения xS+1
– xS
– 1 = 0.
Несложно показать, что при S = 0 выходит деление отрезка напополам, а при S = 1 – знакомое традиционное золотое сечение.
дела примыкающих S-чисел Фибоначчи с абсолютной математической точностью совпадают в пределе с золотыми S-пропорциями! Другими словами золотые S-сечения являются числовыми инвариантами S-чисел Фибоначчи.
7.Золотое сечение в искусстве.
7.1. Золотое сечение в живописи.
Переходя к примерам «золотого сечения» в живописи, недозволено не приостановить собственного внимания на творчестве Леонардо да Винчи. Его Личность – одна из загадок истории. Сам Леонардо да Винчи гласил: «Пусть никто, не будучи математиком, не дерзнет читать мои труды».


Портрет Монны Лизы (Джоконды) долгие годы завлекает внимание исследователей, которые нашли, что композиция рисунка базирована на золотых треугольниках, являющихся частями правильного звездчатого пятиугольника..
Также пропорция золотого сечения проявляется в картине Шишкина. На данной для нас известной картине И. И. Шишкина с очевидностью просматриваются мотивы золотого сечения. Ярко освещенная солнцем сосна (стоящая на первом плане) разделяет длину картины по золотому сечению. Справа от сосны — освещенный солнцем пригорок. Он разделяет по золотому сечению правую часть картины по горизонтали.
В картине Рафаэля «Избиение малышей» просматривается иной элемент золотой пропорции — золотая спираль. На предварительном эскизе Рафаэля проведены красноватые полосы, идущие от смыслового центра композиции — точки, где пальцы вояки сомкнулись вокруг щиколотки малыша — вдоль фигур малыша, дамы, прижимной его к для себя, вояки с занесенным клинком и потом вдоль фигур таковой же группы в правой части эскиза. Непонятно, строил ли Рафаэль золотую спираль либо ощущал её.
Т.Кук употреблял при анализе картины Сандро Боттичелли «рождение Венеры» золотое сеченеие .
7.2. Пирамиды золотого сечения.
Обширно известны мед характеристики пирамид, в особенности золотого сечения. По неким более всераспространенным воззрениям, комната, в какой находится таковая пирамида, кажется больше, а воздух — прозрачнее. Сны начинают запоминаться лучше. Также понятно, что золотое сечение обширно применялась в архитектуре и скульптуре. Примером тому стали: Пантеон и Парфенон в Греции, строения архитекторов Баженова и Малевича
8. Заключение.
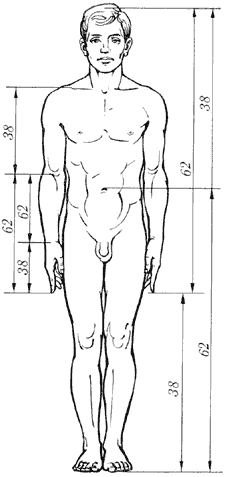

Было подтверждено, что тело человека делится в пропорции золотого сечения линией пояса.
Раковина наутилуса завернута подобно золотой спирали.
Благодаря золотому сечению был открыт пояс астероидов меж Марсом и Юпитером – по пропорции там обязана находиться ещё одна планетка.
Возбуждение струны в точке , делящей её в отношении золотого деления, не вызовет колебаний струны, другими словами это точка компенсации.
На летательных аппаратах с электромагнитными источниками энергии создаются прямоугольные ячейки с пропорцией золотого сечения.
Джоконда построена на золотых треугольниках, золотая спираль находится на картине Рафаэля «Избиение малышей».
Пропорция найдена в картине Сандро Боттичелли «Рождение Венеры»
Понятно много памятников архитектуры, построенных с внедрением золотой пропорции, в том числе Пантеон и Парфенон в Афинах, строения архитекторов Баженова и Малевича.
Иоанну Кеплеру, жившему 5 веков вспять, принадлежит выражение: «Геометрия владеет 2-мя величавыми сокровищами. 1-ое — это аксиома Пифагора, 2-ое — деления отрезка в последнем и среднем отношении»
Перечень литературы
1. Д. Пидоу. Геометрия и Искусство. – М.: Мир, 1979.
2. Журнальчик «Наука и техника»
3. журнальчик «Квант», 1973, № 8.
4. Журнальчик «Математика в школе», 1994, № 2; № 3.
5. Ковалев Ф.В. Золотое сечение в живописи. К.: Выща школа, 1989.
6. Стахов А. Коды золотой пропорции.
7.Воробьев Н.Н. «Числа Фибоначчи» — М.: Наука 1964
8. «Математика — Энциклопедия для деток» М.: Аванта +, 1998
9. информация из веба.
]]>
