Учебная работа. Реферат: Существование решения дифференциального уравнения и последовательные приближения
Выполнил студент 2 курса 1222 группы Труфанов Александр Николаевич
Государственное образовательное учреждение высшего проф образования «Самарский муниципальный институт»
Механико-математический факультет
Кафедра дифференциальных уравнений и теории управления
Самара 2004
Аксиома существования и единственности решения уравнения
Пусть дано уравнение
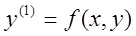
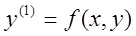
с исходным условием
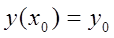
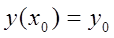
Пусть в замкнутой области R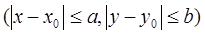
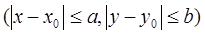
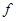
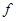
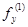
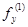
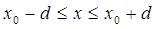
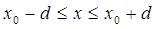
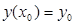
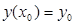
функции 
и 
непрерывны). Тогда на неком отрезке 
существует единственное решение, удовлетворяющее исходному условию 
.
Поочередные приближения определяются формулами:
k = 1,2….
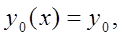
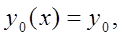
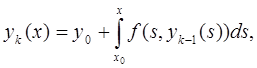
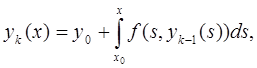
Задание №9
Перейти от уравнения
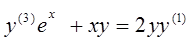
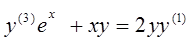
к системе обычного вида и при исходных критериях
, 
, 
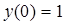
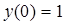
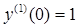
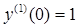
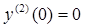
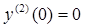
выстроить два поочередных приближения к решению.
Произведем подмену переменных
; 
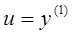
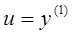
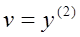
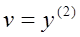
и перейдем к системе обычного вида:
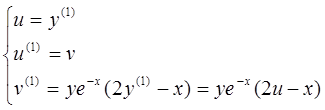
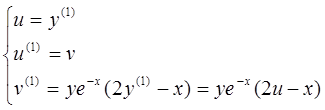
Построим поочередные приближения
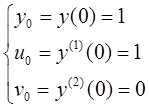
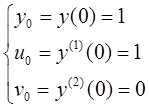
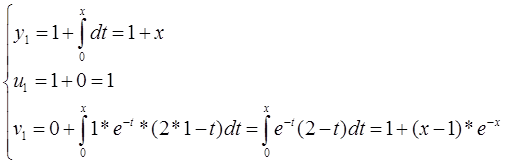
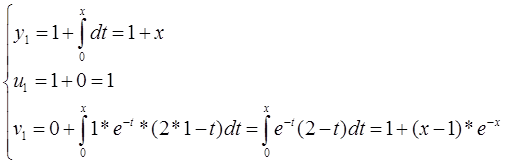
Задание №10
Выстроить три поочередных приближения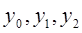 
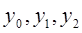
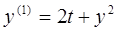
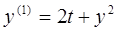
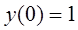
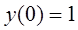
к решению задачки
, 
Построим поочередные приближения
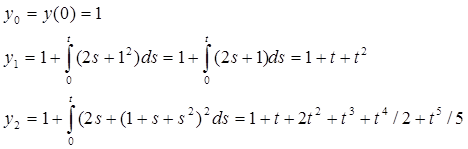
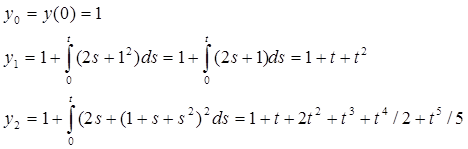
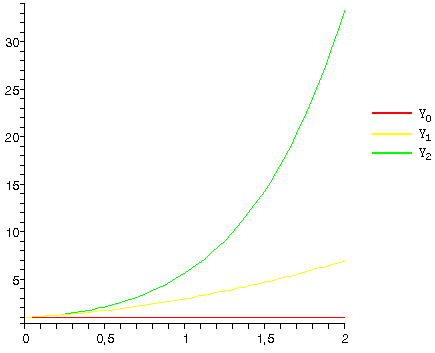
Задание №11
а) Задачку
, 
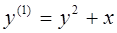
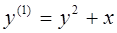
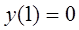
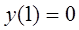
свести к интегральному уравнению и выстроить поочередные приближения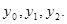 
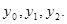
б) Указать какой-нибудь отрезок, на котором сходятся поочередные приближения, и обосновать их равномерную сходимость.
Сведем данное уравнение к интегральному :
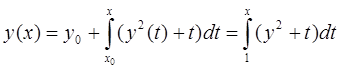
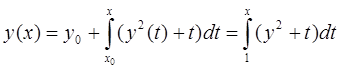
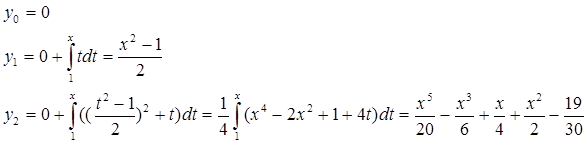
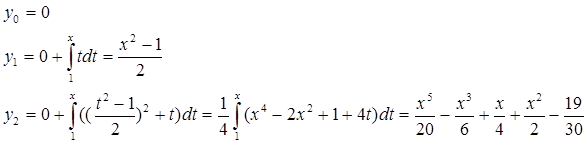
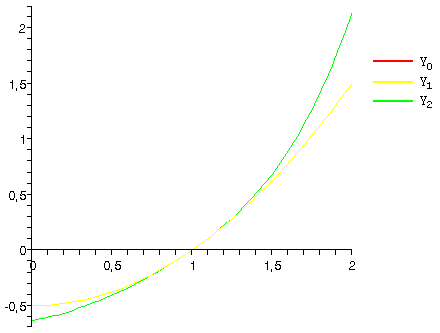
Докажем равномерную сходимость поочередных приближений
При помощи способа поочередных приближений мы можем выстроить последовательность
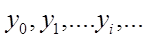
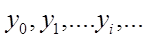
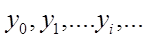
непрерывных функций, определенных на неком отрезке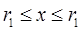 
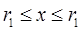
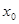
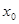
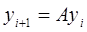
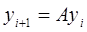
, который содержит снутри себя точку 
. Любая функция последовательности определяется через предшествующую с помощью равенства
i = 0, 1, 2 …
Если график функции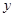 
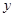
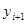
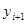
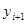
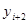
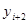
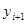
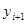
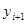
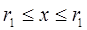
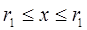
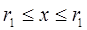
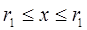
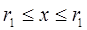
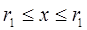
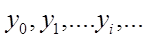
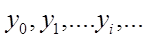
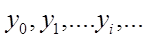
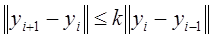
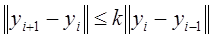
проходит в области Г, то функция 
определена сиим равенством, но для того, чтоб могла быть определена последующая функция 
, необходимо, чтоб и график функции проходил в области Г. Этого удается достигнуть, выбрав отрезок 
довольно маленьким. Дальше, за счет уменьшения длины отрезка , можно достигнуть того, чтоб для последовательности производились неравенства:
, i = 1, 2, …,
где 0 < k < 1. Из этих неравенств вытекает последующее:
, i = 1, 2, …,
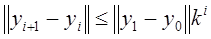
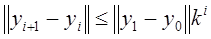
Разглядим нашу функцию на довольно малом отрезке, содержащим 
, к примеру, на 
. На этом промежутке все поочередные приближения являются непрерывными функциями. Разумеется, что т.к. каждое приближение представляет из себя функцию от нескончаемо малого наиболее высочайшего порядка, чем предшествующее приближение, то производятся и описанные выше неравенства. Из этих неравенств следует:
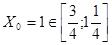
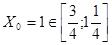
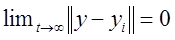
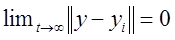
что и является условием равномерной сходимости поочередных приближений.
С иной стороны, на нашем отрезке производится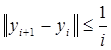 
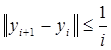
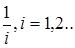
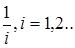
, что также совсем разумеется. А потому что последовательность 
сходится, то последовательность приближений является умеренно сходящийся на этом отрезке.
Перечень литературы
Л.С. Понтрягин. «Простые дифференциальные уравнения», М.: Государственное издательство физико-математической литературы, 1961
А.Ф. Филиппов «Сборник задач по дифференциальным уравнениям», М.: Интеграл-Пресс, 1998
О.П. Филатов «Лекции по обычным дифференциальным уравнениям»,Самара: Издательство «Самарский институт», 1999
А.Н. Тихонов, А.Б. Васильева «Дифференциальные уравнения», М.: Наука. Физматлит, 1998
]]>