Учебная работа. Реферат: О развитии математики в XIX столетии. Гамильтон

Учебная работа. Реферат: О развитии математики в XIX столетии. Гамильтон

.

Христиан Феликс Клейн

Гамильтон

Вильям Роуан Гамильтон родился в 1805 г. в Дублине. Как и Сальмон, он вышел из Тринити-колледжа, который искрометно закончил в ранешней юности. Уже в 1827 г. он получил почетную и видную должность директора обсерватории в Денсинке близ Дублина со званием царского астролога Ирландии. Пост этот он сохранял до конца собственной жизни (1865 г.)

Гамильтон владел необыкновенной по блеску, многогранной даровитостью, замечательнейшим образом проявившейся уже в ранешние его годы. В десятилетнем возрасте он назубок знал Гомера, начал учить арабский язык и санскрит; уже через пару лет он знал тринадцать языков, которыми обладал в совершенстве. При всем этом он имел настолько же очень развитые художественные наклонности; до самых поздних лет он был очень плодовитым поэтом и в течение всей жизни находился в дружественных отношениях с Водсвортом. Тот, кто желал бы ближе познакомиться с личностью Гамильтона и с историей его развития, с наслаждением прочитает толстую трехтомную биографию, размещенную в 1882-1889 гг. Р.П. Грейвзом. Но, будучи написана не математиком, она наиболее посвящена Гамильтону как человеку, нежели как ученому. О конце актуального пути Гамильтона в ней нет никаких подробностей. Как мне ведали в Дублине, в свои крайние годы он вел себя удивительно, чтоб не сказать безрассудно; видимо, его очень рано развившийся стремительно перенапрягся и исчерпал себя ранее, чем о этом можно было бы пошевелить мозгами судя по его возрасту. Творчество Гамильтона владеет соответствующей чертой – везде в его работах рассыпаны новейшие, смышленые наметки, которые потом теряются посреди подробностей, так и не приводя ни к какому полному, завершенному результату.

Как и все прочее, математический творческий процесс начался у Гамильтона в весьма ранешном возрасте. Приблизительно с 1824 по 1825 г. он занимался неуввязками геометрической оптики и аналитической механики. Его заслуги в этих областях мы разглядим несколько позднее.

Начиная с 1833 г. он все наиболее углубляется в рассмотрение сути алгебраической алгорифмики. Его идеи в этом направлении были в первый раз изложены в работе “Theory of conjugate functions or Algebraic Couples; with a preliminary and elementary essay on Algebra as the Science of pure time” (“Теория сопряженных функций либо алгебраических пар; с подготовительным и простым рассуждением о алгебре как науке о чистом времени“), размещенной в 17-м томе “Transactions of Royal Irish Academy” за 1833 и 1836 гг. (см. стр 293 и дальше).

Как это и следует из наименования, понятие числа рассматривается тут как нечто такое, для чего же значимым является время, а не место, поэтому что поначалу речь идет о одной только идее следования – идея эта идет от Канта, но Гамильтон прослеживает ее несколько далее. Количественное, пространственное, исходя из убеждений Гамильтона, заходит в круг наших представлений только с введением вычитания, с помощью которого становится вероятным измерение. Потом разбирается запись x + iy; деяния над всеохватывающими числами – как это сейчас принято именовать везде – он трактует как оперирование по неким, вводимым по соглашению, правилам с числовыми парами (x, y). Вослед за сиим идут общие аксиоматические рассмотрения, касающиеся обыденных арифметических действий, похожие на наиболее поздние конструкции Грассмана.

С этого времени Гамильтон с все огромным энтузиазмом занимается вопросцем о том, может быть ли – методом введения каких-то новейших всеохватывающих чисел – перенести на вариант места, т.е. на вариант нашего обыденного R3
, оказавшуюся таковой полезной геометрическую интерпретацию (на плоскости) действий над числами вида x + i y. Его неустанные усилия в конце концов привели его в 1843 г. к открытию кватернионов – специально устроенных четырехчленных чисел, исследованию и распространению которых он отныне на сто процентов предназначил всего себя. Теория этих чисел изложена им в последующих 2-ух серьезных трудах:

1. “Lectures on Quaternions” (“Лекцииокватернионах”), Дублин, 1853 г.

2. “Elements of Quaternions” (“Элементы теории кватернионов”), Лондон, 1866 г. (посмертное издание).

Весьма скоро в математическом Дублине Энтузиазм к кватернионам стал превалировать над всем остальным; по ним был установлен особый экзамен, и без их познания невообразимо было окончание института. Сам Гамильтон сделал их кое-чем вроде ортодоксальной части собственного математического кредо и подгонял под их все свои геометрические и остальные интересы тем посильнее, чем больше к концу жизни стоновился однобоким и омрачался действием алкоголя его ничего не могла вызвать, не считая противодействия, и поэтому кватернионы – к примеру, в Германии – встречали упрямое сопротивление со стороны большинства математиков, пока они все-же кружным методом, через физику, не просочились в виде векторного анализа, нужного сначала в динамике. И если б нам необходимо было высказать о их сейчас наше суждение, то пришлось бы сказать нечто вроде того, что кватернионы неплохи и полезны на собственном месте, но что все таки они не имеют такового значения, которое имеют обыденные всеохватывающие числа.

И если сейчас я расскажу о кватернионах – как я их уяснил для себя с течением времени – несколько наиболее тщательно, то я буду придерживаться при всем этом обычных нам мыслях и буду сознавать, что я не только лишь становлюсь на точку зрения, резко обратную позиции гамильтонианцев, учитель которых придал всоему открытию совершенно иной наружный вид, но что исходя из убеждений данной нам партии я и на данный момент не имею права именовать кватернионами то, о чем я собираюсь гласить (и что наиболее тщательно изложено в первой тетради “Теории волчка”). Но я очень нередко убеждался в тщетности попыток достигнуть тут какого-нибудь взаимопонимания, чтоб принимать в расчет эти возражения.

Я буду исходить из геометрической интерпретации чисел вида x + i y на плоскости. Как понятно, число x + i y обозначает как точку с координатами x и y, так и отрезок, соединяющий эту точку с началом координат. Сложение

(x + i y) + (a + i b) = (x + a) + i (y + b)

изображается сложением 2-ух направленных отрезков, а означает, быть может интерпретировано как параллельный перенос всей плоскости на отрезок (a + i b). Умножение же

вызывает вращение плоскости вокруг начала координат на угол с одновременным удлинением всех отрезков в отношении , другими словами является сочетанием гомотетии с вращением, либо, как мы будем гласить, – растяжением с вращением (Drehstreckung).

Таковым образом, сложение и умножение, взятые вместе, обхватывают совокупа всех вероятных движений плоскости и даже – с учетом растяжения – несколько больше. Отсюда и вытекает необходимость внедрения в вопросцах метрической геометрии алгебраических вычислений с обычными для нас всеохватывающими числами.

А сейчас возникает вопросец о том, каким образом с помощью соответствующих действий над какими-нибудь всеохватывающими числами наиболее высочайшего типа могут быть изображены надлежащие преобразования в случае места. Для начала можно попробовать разглядеть какое-нибудь трехчленное выражение, обозначая средством точку с координатами x, y, z либо же отрезок – а мы говорим: вектор, соединяющий эту точку с началом координат. (термин “вектор” в первый раз возникает у Гамильтона, в “Quarterly Journal”, 1845, т. I, стр. 56.).

Как и в случае плоскости, сложение 2-ух таковых векторов изображает параллельный перенос места. Но с умножением дело обстоит по другому. Конкретно, вращение вокруг начала координат в пространстве описывает некую ось, и поэтому растяжение с вращением, которое в случае плоскости добивалось 2-ух констант, в пространстве быть может охарактеризовано только 4-мя параметрами:

два из их определяют направление оси вращения: , при этом ;

один обрисовывает угол поворота и

один обрисовывает растяжение r.

Гамильтон строит четырехчленный агрегат – кватернион:

Чисто числовую часть t этого кватерниона он именует скалярной, а направленную часть ix + jy + kz – векторной частью кватерниона. Незапятнанный вектор выходит при , откуда следует, что в данной нам теории он быть может истолкован 2-мя методами: 1) как отрезок; 2) как растяжение с вращением на 1800, которое мы, чтоб быть поочередными, назовем “растяжением с перевертыванием” (“Klappstreckung”).

Пункт 2) снова разъясняет нам, почему для того, чтоб изобразить растяжение с вращением в пространстве, недостаточно незапятнанного вектора (трехчленного выражения): таковой вектор мог бы обрисовывать поворот лишь на 1800; для поворота на случайный угол требуется конкретно кватернион с его скалярной частью.

Очень броско, что задачка описания общего растяжения с вращением в случае места, другими словами задачка композиции 2-ух таковых преобразований, была практически в то же самое время (в 1840 г.) решена Олиндом Родригесом (см. журнальчик Лиувилля, т. 3), который исходил из совсем другой точки зрения. Но еще наиболее поражает, что, как показало рукописное наследство Гаусса, он владел сиим решением уже в 1819 г. На стр. 357 и последующих восьмого тома его “Трудов” имеются заметки о этом преобразовании, которое он именует “мутацией” места.

Но в то время как все упомянутые создатели, складывая два растяжения с вращением, опираются на геометрические суждения, Гамильтон начинает с чисто формального умножения собственных кватернионов, подчиняя его определенным правилам. Как и Грассман, он отрешается от коммутативности умножения, полагая

i2
= j2
= k2
= -1,

jk=i, ki=j, ij=k,

kj=-i, ik=-j, ji=-k

Что все-таки касается остального, то его умножение дистрибутивно, так что

(d+ia+jb+kc)(t+ix+jy+kz)=

=dt-ax-by-cz+i(at+dx+bz-cy)+

+j(bt+dy+cx-az)+k(ct+dz+ay-bx)

Векторы, а именно, перемножаются последующим образом:

(ia+jb+kc)(ix+jy+kz)=

=-(ax+by+cz)+i(bz-cy)+j(cx-az)+k(ay-bx)

Абсолютная, скалярная часть этого кватерниона по терминологии, идущей от Грассмана, именуется внутренним произведением 2-ух начальный векторов, а векторная часть – их наружным произведением. Таковым образом, внутреннее произведение представляет собой скаляр, а наружное – вектор.

Я желал бы сходу же направить внимание на три принципиальных различия, имеющихся меж грассмановым комбинаторным произведением и гамильтоновским подходом:

1. У Грассмана произведение 2-ух единиц eiej не выражается через главные единицы. У Гамильтона же, напротив, эти произведения являются функциями – при этом даже линейными – начальных единиц. Величины высших порядков у него не возникают. В итоге всего этого постановка вопросца о построении системы высших всеохватывающих чисел становится несколько другой. Вычисления с кватернионами можно мыслить для себя с произвольным повторением операций сложения и умножения, что в грассмановой системе не допускается.

2. Грассман с самого начала движим энтузиазмом к n-мерному месту, чего же совсем нет у Гамильтона.

3. У Гамильтона по сопоставлению с Грассманом есть, но, одно доп понятие – понятие поля – делающее кватернионы необходимыми исходя из убеждений физики.

Обе части кватерниона Гамильтон разглядывает как функции точки; он представляет для себя, что к каждой точке места приложен кватернион, другими словами скаляр и вектор. К такому полю кватернионов

t(x,y,z)+iu(x,y,z)+jv(x,y,z)+kw(x,y,z)

он применяет определенные операции, в итоге чего же появляются новейшие поля. Операции эти Гамильтон, следуя специальной, разработанной в Кембридже методике, изображает при помощи так именуемых “символических обозначений”. Скажем, аксиому Тейлора в кембриджской школе принято было записывать в виде

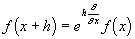
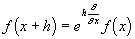
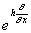
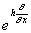
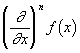
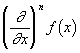
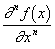
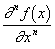
где выражение полагалось мыслить расписанным по правилу разложения показательной функции в ряд, а входящие в него произведения означали личные производные .

Применяя этот метод и тут, Гамильтон строит из личных производных по координатам точки поля так именуемые символические “операторы”. Важным из их является оператор, обозначенный Гамильтоном знаком и нареченный им, вследствие сходства с одним старым музыкальным инвентарем, “наблой”:

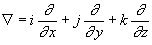
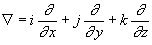
Формально с данной нам наблой обращаются так, как если б она была вектором. Будучи использована к полю кватернионов, она немедля приводит к ряду важных понятий векторного анализа. Так, к примеру, если t – скаляр, то

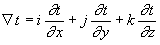
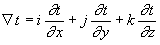
является вектором, “градиентом t”, указывающим в каждой точке величину и направление большего возрастания t.

Будучи использована к вектору iu+jv+kw, операция дает кватернион

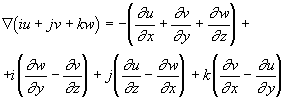
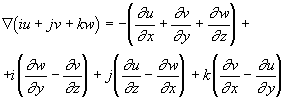
Скалярная часть этого кватерниона именуется дивергенцией поля, а векторная – его вихрем.

Попытка объяснить тут то исключительное очень далековато. Я укажу только, что двукратное применение оператора к скаляру приводит к скаляру

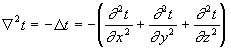
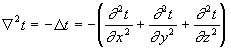
играющему фундаментальную роль в теории потенциала.

Легкость и изящество, с которыми получаются тут глубочайшие по собственному содержанию аксиомы, вправду поразительны. Сиим и разъясняется восхищение кватернионистов собственной системой, восхищение, которое отвергало все другое и, как уже отмечалось, скоро вышло за границы разумного так, что сделалось наносить вред не только лишь арифметике в целом, да и самой теории кватернионов. Такому развитию событий содействовал и доведенный до совершенства, с благоговейным почитанием возделываемый формализм. Появились огромные надежды на предстоящее планомерное развитие данной нам теории по обычным математическим образчикам. К построенному на базе 4 арифметических действий исчислению кватернионов обязана была примкнуть алгебра с тщательно разработанной теорией уравнений вида P(x1
, x2
, …, xn
)=0, где P(x1
, x2
, …, xn
) – многочлен, зависящий от кватернионов x1
, x2
, …, xn
. Конечной целью явилось – и остается доныне – построение теории функций кватернионов, от которой ожидали совсем новейших, необыкновенных по собственному охвату открытий общематематического значения. Чтоб способствовать достижению данной нам цели, не весьма определенной, но принятой с верой в нее, в 1895 г. был даже основан «Глобальный альянс в поддержку кватернионов»! Независимо даже от того, что постоянно наиболее верно скептически относиться к такового рода культивированию и насаждению какого-нибудь 1-го научного направления, сейчас уже можно с определенностью утверждать, что предприятие это обязано считаться потерпевшим крушение либо, во всяком случае, бесплодным. Следование по набросанному выше пути – который претендовал на новизну, хотя практически сводился к практически буквальному перенесению издавна узнаваемых мыслях на единственный объект и, означает, совершенно не содержал внутри себя никакой превосходной концепции – повело ко всякого рода обобщениям узнаваемых теорем, которые при таковой общности теряли свою специфику и становились беспредметными. Лишь в отдельных вариантах вышли личные результаты, доставляющие известное ублажение. Так, к примеру, оказалось, что в области кватернионов не имеет места основная аксиома алгебры, зато любой кватернион удовлетворяет некому кубическому уравнению.

Критика; матричное исчисление Кэли.

Но, упорно следуя намеченным методом, кватернионисты упустили из виду наиболее глубочайшие трудности, представлявшие для науки действительный Энтузиазм. Так, из-за собственной предвзятости они не сообразили того обычного факта, что, кинув на сложившуюся ситуацию взор сверху, они заполучили бы ясное вкупе с этими ораничениями они получили бы и точные указания относительно ведущего к успеху пути.

Сиим наиболее глубочайшим пониманием создавшегося положения вещей мы должны Кэли. В собственной работе «A Memoir on the Theory of Matrices» («Мемуар по теории матриц»; Philosophical Transactions, 1858) он развил некое матричное исчисление, имеющее дело с 4-, 9-, 16-, n2
– членными всеохватывающими числами и в качестве личного варианта обхватывающее также и кватернионы. Деяния над матрицами отталкивалются у Кэли от весьма обычной идеи, состоящей в том, что с матрицами, возникающими в теории линейных подстановок, следует обращаться по правилам, инспирированным данной нам теорией. Соответственно этому сложение 2-ух матриц обязано осуществляться сложением соответственных их частей:

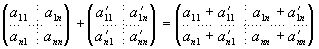
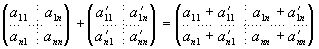
Умножение же матриц делается поочередным выполнением представляемых ими подстановок, другими словами по отлично известному правилу умножения определителей. В случае, когда n = 2,

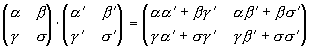
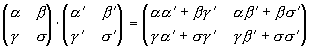
Правило перемножения кватернионов содержится в этом правиле в качестве личного варианта.

По правде, будем осознавать под i обыденный квадратный корень из -1 и положим

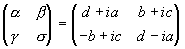
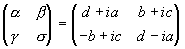
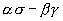
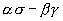
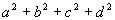
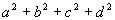
так что определитель окажется равным

Положим соответственно

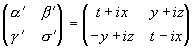
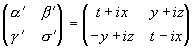
и выполним умножение по обозначенному правилу, принимая во внимание, что i2
=-1. Тогда получится некая новенькая матрица, имеющая вид

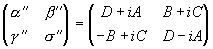
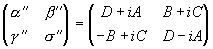
где четыре величины A, B, C и D имеют последующие значения:

A = dx + at + bz – cy

B = dy – az + bt + cx

C = dz + ay – bx + ct

D = dt – ax – by – cz

Таковым образом, мы вправду по двум кватернионам d+ix+jy+kz и t+ix+jy+kz выстроили 3-ий, который выходит из их умножением по Гамильтону.

Итог этот, сначала кажущийся нежданным, при ближнем рассмотрении оказывается полностью понятным, если исходить из геометрического существа рассматриваемой ситуации. Так как деяния над кватернионами тем представляют собой не что другое, как оперирование с бинарными линейными подстановками, мы можем заключить, что для плодотворного внедрения кватернионов соответствующим является вариант, когда в рассмотрении участвуют такового рода подстановки. Это разъясняет, а именно, почему кватернионы так полезны в теории растяжений с вращением. Каждое растяжение с вращением оставляет недвижной надуманную сферическую окружность, другими словами геометрический образ, точки которого правильно выражаются через один-единственный параметр 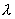. 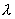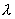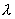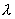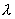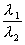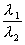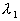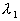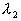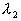Потому, если записать в однородном виде , то при растяжении места с одновременным его вращением характеристики , подвергаются бинарной линейной подстановке.

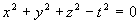
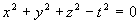
Схожим образом разъясняется и сияние, с которым кватернионы используются в теории относительности. тут инвариантной оказывается поверхность второго порядка в R4
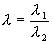
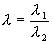
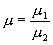
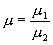
. Эта поверхность несет два семейства прямых, каждое из которых описывается одним параметром либо . При растяжении с вращением любой из этих характеристик подвергается бинарной линейной подстановке.

]]>