Учебная работа. Реферат: Исследование свойств прямоугольного тетраэдра
Общеобразовательная городская средняя школа №5
город Кузнецк, 2004 год
І. Объект исследования
В работе в первый раз вводится понятие «Прямоугольный тетраэдр». Тетраэдр- полиэдр, содержащий 4 грани. Тетраэдр является треугольной пирамидой и содержит 4 трёхгранных угла (рис. 1) Трёхгранный угол- фигура, образованная 3-мя плоскостями (гранями), имеющими общую точку (верхушку) (рис 2) [1,2].
О О
А В
А В
С С
Рис. 1 Тетраэдр. Рис. 2 Трёхгранный угол.
Трёхгранный угол содержит три плоских угла, образованных рёбрами, лежащими на одной грани. Введем понятие прямого трехгранного угла. Назовем прямым трёхгранным углом трехгранный угол, содержащий три прямых плоских угла (рис3), т.е. рёбра трёхгранного угла взаимно перпендикулярны. Введем также понятие прямоугольного тетраэдра. Тетраэдр именуется прямоугольным, если содержит прямой трёхгранный угол (рис 4).
А А
В В
О О
С
Рис. 3 Схема прямого Рис. 4 Схема прямоугольного
трёхгранного угла, тетраэдра.
Введем также понятия катетных граней, гипотенузной грани, катетов и гипотенуз прямоугольного тетраэдра. Прямоугольный тетраэдр содержит три катетные грани (грани, содержащие прямой тонкий угол) и гипотенузную грань (не содержащую прямой угол). Прямоугольный тетраэдр содержит три катета (рёбра прямого трёхгранного угла) и три гипотенузы (рёбра, лежащие на гипотенузной грани). Тетраэдр, катеты которого равны, назовем равнокатет-ным.
Іі. Цель исследования
установление либо подтверждение параметров прямоугольного тетраэдра
Актуальность темы: прямоугольный тетраэдр является простейшей геометрической фигурой, обладающей неповторимыми качествами. исследование этих параметров в школьном курсе арифметики обязано содействовать развитию абстрактного и логического мышления у учащихся.
ІІІ. Подтверждения параметров прямоугольного тетраэдра.
I. Квадрат площади гипотенузной грани равен сумме квадратов площадей катетных граней.
А
Дано:
ОАВС — прямоугольный тетраэдр
SОАВ= S1 SABC= S
SOBC= S2 SOAC= S3 В
Обосновать: О
D
S²=S1²+S2²+S3²
С
подтверждение.
Пусть AD- высота гипотенузной грани АВС, проведённая к ребру ВС из верхушки А, ОD- II
. Сумма квадратов гипотенуз равна двойной сумме квадратов катетов.
Дано: А
ОАВС- прямоугольный тетраэдр
где а , b , с — катеты. В
АВ, ВС и АС- гипотенузы а
Обосновать: b
АВ²+ВС²+АС²=2(а² + b² +с²)
подтверждение. О
АВ² = а² + b² с С
ВС² = b² + с² (по аксиоме Пифагора)
АС² = а² + с²
АВ² + ВС² + АС² =2а² + 2 b² +2с² , что и требовалось обосновать.
III. Объём прямоугольного тетраэдра равен 1/6 произведения катетов.
А
Дано:
ОАВС — прямоугольный тетраэдр
а , b , с — катеты. В
Обосновать: а b
V=(1/6) а · b · с
подтверждение. О С
с
Так как тетраэдр является треугольной пирамидой, его объём
V=(1/3 )Sосн · h
Выберем в качестве основания катетную грань ОВС, тогда катет а будет высотой тетраэдра, т.к. а перпендикулярен ОВС, т.е.
V=(1/3) SOBC· а , т.к.SOBC=(1/2) b·.с
Имеем V=(1/6) а · b · с, что и требовалось обосновать.
Расстояние от верхушки прямого трёхгранного угла до гипотенузной грани определяется по формуле:
h = (a۰b۰c)/√a²·b² + b²·c² + a²·c²
где a, b, c – катеты тетраэдра
Дано: А
ОАВС- прямоугольный тетраэдр
ОА = а, ОВ = b, ОС = с катеты Д
ОД = h – перпендикуляр к грани
АВС а
h В
Обосновать: b
____________ О
h = (a·b·c) / √a²b²+b²c²+a²c² сС
подтверждение.
Размер тетраэдра:
V = (1/3)SАВС
·h
C иной стороны: V = (1/6)abc (свойство 3 прямоугольного тетраэдра).
Как следует,
h = (abc) / (2SАВС
)
Из первого характеристики прямоугольного тетраэдра:
___________________
SАВС
= √Ѕ²ОАВ
+ S²ОВС
+S²ОАС
____________
т.е. SАВС
= (1/2)√a²b²+b²c²+a²c²
Как следует,
____________
h = (abc) / √a²b²+b²c²+a²c² , что и требовалось обосновать.
Косинусы направляющих углов нормали к гипотенузной грани определяются по формулам:
____________
cos α = h / a= (bc)/√a²b²+b²c²+a²c²
____________
сos β = h / b = (ac) / √a²b²+b²c²+a²c²
____________
cos γ = h /c= (ab)/√a²b²+b²c²+a²c²
где a, b, c – катеты тетраэдра;
α – угол меж катетом а и нормалью
β – угол меж катетом b и нормалью
γ – угол меж катетом с и нормалью.
h – нормаль
Дано:
ОАВС — прямоугольный тетраэдр.
ОА = а, ОВ = b, ОС = с — катеты
ОД = h – нормаль к грани АВС А
Обосновать: Д
____________
cosα = (bc) / √a²b² +b²c² +a²c² h
____________ а В
cosβ = (ac) / √a²b² +b²c² +a²c² α b
____________ β
cosγ = (ab) / √a²b² +b²c² +a²c² γ
С
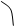
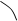
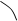
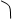
О с
подтверждение.
Соединим точку Д с точкой А и получим прямоугольный треугольник ОАД
cos α = ОД/ОА = h/a
____________
Так как h = (abc) / √a²b²+b²c²+a²c²
____________
cosα = (bc)/√a²b²+b²c²+a²c² , что и требовалось обосновать.
Аналогично:
____________
cosβ = ОД/ОВ = d/b = (ac)/√a²b²+b²c²+a²c²
____________
cos γ = ОД/ОС = d/c = (ab)/√a²b²+b²c²+a²c²
Радиус сферы, описывающей прямоугольный тетраэдр, определяется по формуле:
________
R = ( ½) · √a²+b²+c²
где a, b, c – катеты тетраэдра
К L
Дано:
ОАВС- прямоугольный тетраэдр А М
ОА = а, ОВ = b, ОС = с – катеты
R – радиус сферы, описывающей
тетраэдр.
Обосновать: а
_______ В Д
R = (1/2)√a²+b²+c² b
О
подтверждение. с С
На базе прямоугольного тетраэдра
ОАВС достраиваем прямоугольный параллелепипед ОВДСАКЛМ. Диагонали прямоугольного параллелепипеда являются поперечниками описывающей его сферы, т.к. центр симметрии прямоугольного параллелепипеда совпадает с центром описанной сферы т.е.:
_______ _____ ________
КС = D = √a²+b²+c² (ВС = √b²+c² , ВК = а, КС = √ВС²+ВК² )
Так как данная сфера сразу обрисовывает прямоугольный
тетраэдр, имеем:
_______
R = (1/2)D = (1/2)√a²+b²+c²,
что и требовалось обосновать.
VII. Радиус сферы, вписанной в прямоугольный тетраэдр, определяется по формуле:
abc
r = ____________ ,
√a²b²+b²c²+a²c² + ab + bc + ac
где a, b, c — катеты тетраэдра.
Дано: ОАВС — прямоугольный тетраэдр
ОА = а, ОВ = b, ОС = с – катеты. О1
– центр вписанной сферы
r — радиус вписанной сферы
Обосновать:
r = h / (1 + cosα + cosβ + cosγ)
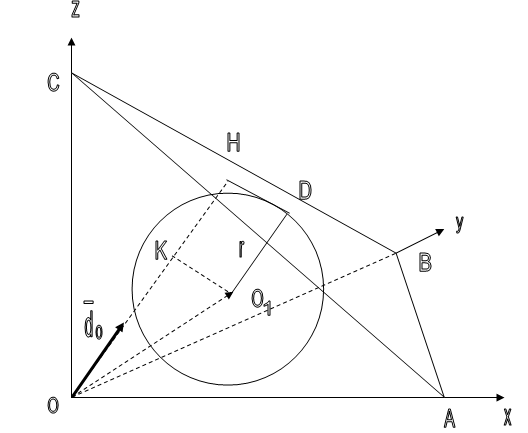
подтверждение: Пусть вписанная сфера касается гипотенузной грани в точке Д. Тогда О1
Д перпендикулярна гипотенузной грани и О1
Д = r.
_ _
Пусть do
— единичный вектор нормали к гипотенузной грани, т.е. |dо
| = 1
Координаты этого единичного вектора (cosα; cosβ; cosγ) являются направляющими косинусами нормали к гипотенузной грани.
__
Найдем проекцию вектора ОО1
с координатами (r; r; r) на вектор нормали:
___ __
ОК = |ОО1
|cosδ , где δ – угол меж вектором ОО1
и вектором нормали.
___ __ _ __ _
|OO1
|cosδ = (OO1
·do
) = r·cosα + r·cosβ + r·cosγ , где (ОО1
·dо
) – скалярное произведение 2-ух векторов.
Пусть перпендикуляр к гипотенузной грани ОН = h,
тогда h = OK + KH, т.е.
h = |OO1
|cosδ + r, т.к. КН = r
(так как КНДО1
является прямоугольником).
Имеем
h = rcosα + rcosβ + rcosγ + r
т.е.
r = h / (1 + cosα + cosβ + cosγ)
С учетом 4-го и 5-го параметров прямоугольного тетраэдра имеем полную формулу:
(abc)/√ a²b²+b²c²+a²c² abc
1 + (bc + ac + ab) / √a²b²+b²c²+a²c² √a²b²+b²c²+a²c² + ab + bc + ac
характеристики равнокатетного прямоугольного тетраэдра.
А
Дано:
ОАВС -прямоугольный тетраэдр
ОА = ОВ = ОС = а – а
катеты В
Обосновать, что гипотенузная а
грань является правильным
треугольником и косинусы О Д
двугранных углов меж
гипотенузной гранью и катетными а
гранями равны С
___
√1/3
подтверждение.
стороны гипотенузной грани находим по аксиоме Пифагора:
_________ __
АС = √ ОА² +OC² = √2 а
_________ __
АВ = √ ОА² +OB² = √2 а
_________ __
ВС = √ ОВ² + ОС² = √2 а
т.е. треугольник АВС равносторонний либо верный, что и требовалось обосновать.
Проведем отрезок АД перпендикулярно ВС. Отрезок ОД является проекцией отрезка АД на грань ОВС и потому ОД будет перпендикулярен ВС по аксиоме о 3-х перпендикулярах. Как следует, угол ОДА является линейным углом двугранного угла меж гранями ОВС и АВС
Так как АД является высотой правильного треугольника АВС:
_ _ _ ___
АД = (√3/2)АВ = (√3/2)√2 а = √3/2 а
ОД является высотой равнобедренного прямоугольного треугольника ОВС, опущенной с верхушки прямого угла. Как следует:
ОД = а/√2
Косинус двугранного угла:
сos_ОДА = ОД/АД = 1/√3 , что и требовалось обосновать.
Результаты исследования: исследования дозволили установить выше 8 важных параметров прямоугольного тетраэдра. Так как эти исследования проводились в первый раз, все приобретенные результаты владеют научной новизной.
Формула, устанавливающая связь меж площадями граней прямоугольного тетраэдра, является аналогом аксиомы Пифагора для трехмерных фигур и потому имеет огромную теоретическую значимость.
І
V
. Практическое применение параметров прямоугольного тетраэдра
Результаты исследовательских работ можно применять при решении задач на факультативных упражнениях по темам «Пирамида» и «Прямоугольный параллелепипед» в средней школе. С внедрением параметров прямоугольного тетраэдра можно отыскать наиболее оптимальные и облегченные варианты решения задач по сопоставлению с классическими способами.
К примеру: задачка №96 (стр.131) учебного пособия: В.М.Клопский, З.А.Скопец, М.И.Ягодовский. Геометрия.-М.: Просвещение, 1979.
Основанием пирамиды служит прямоугольный треугольник с катетами а и b, высота пирамиды проходит через верхушку прямого угла основания и равна Н. Отыскать площадь полной поверхности.
А
Дано:
ОАВС- пирамида,
основанием является прямоугольный H
треугольник ОВС с катетами а и b В
ОА = Н, высота.
Отыскать: b
S полн. О Д
а
С
1) Решение по классической схеме:
S полн. = SАОС
+ SАОВ
+ SВОС
+ SАВС
SАОС
= (1/2)аН; SАОВ
= (1/2)bН; SВОС
= (1/2)аb;
Найдем основание и высоту боковой грани АВС при помощи аксиомы Пифагора:
______ ________
ВС = √ а² +b² ; АД = √ ОД² +Н² , где ОД – Так как ОД _ ВС, из подобия треугольников ВОС и ВОД имеем:
______
ОД/ b = а/ВС либо ОД = (аb)/ВС = (аb)/ √ а² +b²
Как следует, _______________ ________________________
АД = √ (аb)/( а² +b²) + Н² = √[(аb)² +(bH)² + (аH)²]/( а² +b²)
_________________
В итоге получаем SАВС
= (1/2) √ (аb)² +(bH)² + (аH)²
_________________
Cледовательно, S полн.= (1/2) [√ (аb)² +(bH)² + (аH)² + аН + bН + аb]
2) Решение с внедрением первого характеристики прямоугольного тетраэдра:
Sполн.= SАОС
+ SАОВ
+ SВОС
+ SАВС
SАОС
= (1/2)аН; SАОВ
= (1/2)bН; SВОС
= (1/2)аb;
___________________ _________________
SАВС
= √ SАОС
² + SАОВ
² + SВОС
² = (1/2)√ (аb)² +(bH)² + (аH)²
_________________
Cледовательно, S полн.= (1/2)(√ (аb)² +(bH)² + (аH)² + аН + bН + аb)
задачка №280 (стр.76) учебного пособия: Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев и др. Геометрия.-М.: Просвещение, 1994.
Ребро куба равно а. Отыскать площадь сечения, проходящего через диагонали 2-ух его граней
К L
Дано:
ОВДСАКLM — куб А М
ОА = а, ОВ = b, ОС = с – ребра
ΔАВС – сечение куба плоскостью, прохо-
дящей через диагонали смежных а
граней. В Д
Отыскать: а
SАВС
О
а С
1) Решение по классической схеме:
Найдем стороны сечения АВС при помощи аксиомы Пифагора:
______ __
АС = АВ = ВС = √ а² + а² = √2 а
Площадь правильного треугольника АВС найдем по формуле:
_ _ _
SАВС
= (√3/4)(АС)2
, т.е. SАВС
= (√3/4)(2а2
) = (√3/2)а2
2)Решение с внедрением первого характеристики прямоугольного тетраэдра:
SАОС
= SАОВ
= SВОС
= (1/2)а2
(так как тетраэдр равнокатетный);
___________________
SАВС
= √ SАОС
² + SАОВ
² + SВОС
²
_________ _
Cледовательно, SАВС
= (1/2) √ а² + а² + а² = (√3/2)а2
Перечень литературы
М.Я.Выгодский. Справочник по простой арифметике. Изд. 6-е, Гостехиздат, М.-Л., 1952.
А.П.Киселев. Геометрия. Учебник для средней школы, ч.1 и 2.- М.: Учпедгиз1951.
Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев и др. Геометрия. Учебник для средней школы.-М.: Просвещение, 1994.
]]>