Учебная работа. Реферат: Бернулли
Протестантство возникло в Нидерландах скоро опосля известного выступления Лютера 1517 г., направленною против реализации индульгенций. Борьба против испанского ига переплелась с борьбой за свободу исповедания. Народное движение приняло религиозную расцветку и расплескивалось обширнее и обширнее по стране.
В 1550 г. Карл V издал указ против еретиков, поставивший практически всех протестантов вне закона и объявивший неограниченный террор на всей местности Нидерландов.
пришел конец простой законности. С бескрайним цинизмом без суда уничтожались целые семьи, и даже роды. вкупе с казнями состоявшихся людей отторгалось принадлежавшее им имущество, изымались средства и ценности. Началась эмиграция. Она достигнула таковых размеров, что почти все местечки опустели, а в городках численность населения приметно уменьшилась.
Купеческая протестантская семья Бернулли жила в Антверпене. Собственный род она вела из Фландрии, где Бернулли, в XV в. носившие еще фамилию Бернуйла (Bernuilla), не избегали и военных дел. Семья держалась насиженного места, пока можно было рассчитывать на то, что все как-то устроится. Надежды связывались с фуррорами освободительного движения: невзирая на зверства Альбы, северные провинции Нидерландов, объединенные вокруг Вильгельма Оранского, вынудили Филиппа признать их Право на самоопределение. По договору 1579 г. семь северных провинций, образовавших ядро будущей Голландии, освобождались от испанского владычества. Но другие провинции—и город Антверпен, в том числе — оставались под испанской короной.
Тем все надежды рушились. Под опасностью физического поражения приходилось покидать родной город. Большая часть эмигрантов направлялось в прирейнские провинции Германии, поэтому что еще при жизни Карла V Германия достигнула свободы исповедания (Аугсбургский мир 1555 г.). Чудилось, волнения там улеглись и можно будет отдохнуть от десятилетий террора. Семья Бернулли решает двигаться во Франкфурт-на-Майне. Реформация в этом городке прошла еще в 1533 г., господствующая религия—протестантская. Выбор кажется удачным. В 1582 г. семья трогается в путь. Нелегко было порывать с родными местами. Глава семьи, Якоб Бернулли, скончался во Франкфурте в последующем же году.
Расчеты эмигрантов на то, что получится основаться на новеньком месте, не оправдались: и в Германии вражда меж католиками и протестантами не гасла. С начала XVII в. атмосфера безпрерывно сгущалась; в 1618 г. началась Тридцатилетняя война, принесшая с собой невиданные бедствия и расстройство хозяйственных связей. Принято решение было находить размеренного пристанища. Выбор тормознул на Швейцарии, а конкретно на Базеле. Положение в Швейцарии чудилось относительно размеренным: реформация там утвердилась в 20-е годы XVI столетия, религиозные волнения за протекшие 100 лет улеглись. В 1622 г. иной Якоб, внук первого Якоба, переехал в Базель и принял Гражданство Базельской республики. Сейчас эмиграция заканчивается успешно. Отпрыск Якоба Николай уже видное лицо в городке, пользующийся почтением негоциант, глава семьи, состоящей из одиннадцати малышей. Посреди его малышей и находятся те, с кого начинается династия выдающихся математиков.
Чем вызвано переселение Бернулли конкретно в Базель, тяжело сказать. Единственно, что можно утверждать с полной уверенностью, это то, что наличие в городке института не игралось в выборе никакой роли: семья Бернулли из поколения в поколение старалась отвлечь свою молодежь от науки и направить ее дарования на коммерческую деятельность либо адвокатуру. К счастью, молодежь сама выбирала свои пути, не весьма считаясь с желаниями старших.
Посреди Бернулли некие имена повторяются из поколения в поколение, потому их различают, как правителей, присоединив к имени подобающую цифру. Вот родословная Бернулли:
Якоб (1598-1634). Уроженец Франкфурта-на-Майно. В 1622 г. переехал на неизменное жительство в Базель.
Николай (1623-1708). Отпрыск Якоба. Уроженец Базеля. Торговец аптекарскими продуктами и фармацевтическими травками. Член Огромного совета Базеля и член суда. Имел 11 малышей.
Якоб I (1654-1705). Отпрыск Николая. По образованию богослов. С 1687 г. доктор арифметики Базельского института. Учениками Якоба I были: его младший брат Иоганн I, племянник Николай I, член Петербургской академии, механик и математик Я. Герман, отец величавого Л. Эйлера — Пауль Эйлер.
Николай (1662-1716). Брат Якоба I. Живописец. Член суда.
Иоганн I (1667-1748). Брат Якоба I. Десятый ребенок в семье Николая. По образованию доктор. С 1695 г. доктор арифметики Гронингенского института (Голландия). С 1705 г. доктор арифметики Базельского института. Знатный член Петербургской академии.
Жером (1669-1760). Брат Иоганна I. Торговец аптекарскими продуктами.
Николай. Единственный отпрыск Якоба I, имевшего еще дочь. Вопреки желанию отца, уклонился от научной карьеры и стал живописцем. По словам современников, очень средним.
Николай I (1687-1759). Отпрыск Николая. По образованию юрист. доктор арифметики в Падуе, доктор логики и права в Базеле.
Николай II (1695-1726), отпрыск Иоганна I. По образованию юрист. доктор права в Берне, доктор арифметики в Петербурге.
Даниил I (1700-1782). Уроженец Гронингена. Отпрыск Иоганна I. По образованию доктор. В 1725-1733 гг. работал на кафедрах физиологии и механики в Петербургской академии. С 1733 г. доктор по кафедре физиологии , с 1750 г. доктор по кафедре механики в Базеле. Знатный член Петербургской академии.
Иоганн II (1710-1790), Отпрыск Иоганна I. По образованию юрист. доктор элоквенции (сладкоречия), доктор арифметики в Базеле.
Иоганн III (1744-1807). Старший отпрыск Иоганна II. По образованию юрист. Астролог Берлинской академии, там же директор математического класса.
Даниил II (1751-1834). 2-ой отпрыск Иоганна II. По образованию доктор, доктор сладкоречия в Базеле.
Якоб II (1759-1789). 3-ий отпрыск Иоганна II. По образованию юрист. Математик Петербургской академии. Утоп в Неве.
Кристоф (1782-1863). Отпрыск Даниила II. доктор технологии в Базеле.
Иоганн-Густав (1811-1863). Отпрыск Кристофа. доктор технологии в Базеле.
Представители рода Бернулли живут в Базеле и в истинное время.
Якоб (1598-1634)
Николай (1623-1708)
Якоб I (1654-1705) Жером(1669-1760)
Николай(1662-1716) Иоганн I (1667-1748)
Николай
Николай I (1687-1759)
Николай II (1695-1726) Даниил I (1700-1782)
Иоганн II (1710-1790)
Якоб II (1759-1789) Иоганн III (1744-1807) Даниил II(1751-1834)
Кристоф(1782-1863)
Иоганн-Густав(1811-1863)
Якоб I. Родился 27 декабря 1654 г. По желанию отца готовился к званию протестантского священника. Закончил Базельский институт, где изучал философию, Богословие и языки. Обладал германским, французским, английским, итальянским, латинским и греческим языками. Испытывая неодолимое желание к арифметике, изучал ее тайком от отца. В 1671 г. получил степень магистра философии. С огромным фуррором читал проповеди на германском и французском языках. В то же время продолжал пополнять свои познания по арифметике без учителя, практически без учебников.
В октябре 1686 г. оказывается свободной должность доктора арифметики в Базельском институте. Успехи Якоба в арифметике отлично известны, и Сенат института единогласно выдвинул на свободную должность Якоба Бернулли. Вступление в должность состоялось 15 февраля 1687 г. Навряд ли присутствовавшие при всем этом умеренном акте представляли, что они являются очевидцами начала беспрецедентного в истории арифметики действия: с этого момента кафедру будут занимать Бернулли в протяжении 100 лет. Члены же данной для нас семьи будут докторами родного института в течение четверти тысячелетия, прямо до 2-ой половины XX в.
В том же году Якоб Бернулли прочел в «Асtа Eruditirum» за 1684 г. «Новейший способ» Лейбница и, найдя трудные места, письменно обратился к Лейбницу за объяснением. Лейбниц, находившийся в долговременной служебной поездке, получил письмо лишь через три года, когда надобность в консультации отпала: Якоб вместе Иоганном обуяли дифференциальным и интегральным исчислениями так, что скоро смогли приступить периодическому развитию способа. Образовавшийся триумвират — Лейбниц, Якоб и Иоганн Бернулли — наименее чем за 20 лет очень обогатил анализ нескончаемо малых.
С 1677 г. Я. Бернулли стал вести записные книги, куда вносил различного рода заметки научного содержания. 1-ые записи посвящены теологии, изготовлены под воздействием всераспространенного в то время в Базеле сборника спорных теологических вопросцев.
Основное пространство в записных книгах занимает решение задач. Уже по ранешным записям можно судить о проявленном Я. Бернулли интересе к прикладной арифметике. Математические заметки демонстрируют, как равномерно Я. Бернулли завладевал способами Валлиса, Декарта, инфинитезимальными способами, как развивал и улучшал их. Решенные им задачки служили отправными пт для последующих наиболее глубочайших исследовательских работ.
В январе 1684 г. Я. Бернулли провел в Базельском институте открытый диспут, на котором защищал 100 тезисов, из их 34 логических, 18 диалектических и 48 смешанных. Некие тезисы очень любопытны. Вот примеры:
«78. время от времени существует несколько кратчайших путей из точки в точку.
83. .Посреди изопериметрических фигур одна быть может в нескончаемое число раз больше иной.
85. Не в любом треугольнике сумма внутренних углов равна двум прямым.
89. Квадратура круга еще не найдена, но не поэтому, что меж искривленным и прямолинейным нет никакой связи; в реальности кривую можно спрямить, а криволинейную фигуру квадрировать»
В мае 1690 г. Я. Бернулли опубликовал в «Асtа Eruditirum» первую работу, связанную с исчислением нескончаемо малых. В ней он отдал решение поставленной Лейбницем в 1687 г. задачки о парацентрической изохроне. нужно было отыскать кривую, по которой вещественная точка опускалась бы в равные промежутки времени на равные высоты. Я. Бернулли вывел дифференциальное уравнение кривой и проинтегрировал его. При всем этом он в первый раз употребил в печати термин «интеграл», указав, что из равенства 2-ух выражений, связывающих дифференциалы, следует равенство интегралов.
В лекциях, читанных Лопиталю, И. Бернулли ход решения излагает так. Пусть разыскиваемой кривой будет АDС. Вещественная точка за время ∆t {перемещается} из точки D в точку d и из точки С в точку с. По условию задачки проекции дуг Dd Сс на вертикаль схожи. Проведем через D и С касательные к кривой до пересечения с продолжением АF. Отрезки касательных будут DK и CL. Напишем тождество
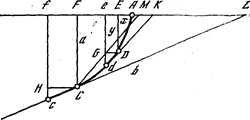
Dd/Сс=Dd/Hc • Hc/Cc.
Дуги Dd и Сс малы, потому фигуры GDd и НСс можно считать треугольниками.
Из подобия треугольников GDd и DEK, НСс и СFL получим
Dd/DG=DK/DE,Сс/Нс=CL/СF.
При помощи этих пропорций найдем
Dd/Сс=DG1Нс • DК/DЕ • СF/СL.
По условиям задачки dG/Нс=1, потому
Dd1Сс=DК/DЕ • СF/СL.
Проведем через точку С прямую СМ, параллельную DК. Тогда
DК/DЕ=СМ/СF, Dd/Сс=СМ/СL.
Но отношение Dd/Сс равно отношению скоростей (интервал ∆t один и этот же), квадраты же скоростей, по отысканному Галилеем закону, относятся как пройденные высоты; это дает
Dd2/Сс2=СМ2/СL2=DЕ/CF, СМ2/СL2 =DЕ/СF.
Крайнее равенство значит, что если через две произвольные точки кривой провести касательные СL и DК и через точку С провести СМ параллельно DК, то обязана производиться обозначенная пропорция. Таковым свойством владеет разыскиваемая кривая.
задачка оказалась сведенной к классу оборотных задач на касательные: отыскать кривую, касательные к которой удовлетворяют некому требованию. Схожую задачку в первый раз предложил Декарту Дебон, и Декарт с ней не совладал. Разработанный Лейбницем способ дозволяет решать и оборотные задачки на касательные.
Выберем начало координат в точке А. Обозначим АЕ=х, ЕD=у. Тогда GD=dх, Gd=dу. Обозначим также СF=а, СL=b. Треугольники FСМ и СdD подобны, отсюда
Gd/Dd=FС/СМ.
Но Dd = √dx2+dy2, потому
dy/√ dx2+dy2= а/СМ, откуда
CM2= (a2dx2+a2dy2)/dy2.
Подставим отысканное выражение в пропорцию СL2/СM2=СF/СЕ и получим дифференциальное уравнение
b2dy2/(a2dx2+a2dy2)=a/y, b2ydy2-a3dy2=a3dx2, (b2y-а3)dу2 = а3dx2,
√b2y-a3 dy=√a3 dx.
В уравнении переменные разбиты, интегрирование его дает разыскиваемую кривую
2b2у — 2а3/3b2 √b2у – а3 == х√а3.
Парацентрическая изохрона оказалась полукубической параболой. Вид кривой ранее Я. Бернулли обусловили Лейбниц и Гюйгенс, но только Я. Бернулли отдал решение средствами анализа нескончаемо малых.
В приложении к иной работе о рядах (1694 г.) Я. Бернулли определил несколько тезисов.
1. Есть спирали, которые совершают нескончаемое число витков вокруг полюса, но имеют конечную длину.
2. Есть кривые, которые, подобно эллипсу, замкнуты и, подобно параболе, уходят в бесконечность, к примеру ay2=х2(b+х).
3. Есть кривые, состоящие из 2-ух веток, к примеру ау2=х{а2—х2),
4. Есть неограниченные поверхности с конечной площадью.
5. Есть неограниченные поверхности с нескончаемой площадью, но такие, что надлежащие им тела вращения владеют конечным объемом.
Я. Бернулли увлекался также и изопериметрическими задачками. Древная из их—задачка знаменитой основоположницы Карфагена и его первой королевы Дидоны. Легенда такая. Дидона бежала от отца, тирского царя, и достигнула Африки, где купила у аборигенов участок земли на берегу моря «не больше, чем можно окружить воловьей шкурой». Она разрезала шкуру на узенькие полосы и связала из их длинноватую ленту. Спрашивается, какой формы обязана быть фигура, оцепленная лентой данной длины, чтоб площадь фигуры была большей?
Ван-дер-Варден пишет, что Зенодор, живший скоро опосля Архимеда, высказал 14 предложений относительно изопериметрических фигур. Он утверждал, что из всех фигур (кругов и многоугольников), имеющих однообразный периметр, круг будет большим, также и то, что из всех пространственных тел с схожей поверхностью большим будет шар.
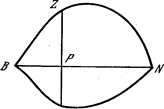
Решение задачки содержится в записных книгах Я. Бернулли и помещено в майском номере «Acta Eruditorum» за 1701 г. Я. Бернулли и тут применил высказанный ранее принцип: так как площадь обязана быть экстремальной, сиим же свойством обязана владеть и неважно какая ее простая часть. Он получил дифференциальное уравнение третьего порядка и потом проинтегрировал его.
К. А. Рыбников пишет: «Таковым образом, решение изопериметрической задачки означало весьма принципиальный, принципно новейший шаг в истории вариационного исчисления; оно отдало возможность решать наиболее сложные вариационные задачки, им был изготовлен принципиальный шаг на пути решения вариационных задач».
При исследовании параметров сочетаний и фигурных чисел Я. Бернулли повстречался с суммированием степеней натуральных чисел Sm = å km
Эти вопросцы заинтересовывали математиков и ранее. Я. Бернулли составил таблицу фигурных чисел, ука зал их характеристики и на основании отмеченных параметров отыскал формулы для сумм степеней натуральных чисел. Он привел формулы сумм от S(п) до S(п10):
S (n) = n2/2 +n/2
S (n2) = n3/3 + n2/2+ n/6
S (n3) = n4/4 + n3/2 + n2/4
S (n4) = n5/5 + n4/2 + n3/3 – n/30
S (n5) = n6/6 + n5/2 + 5n4/12 – n2/12
S (n6) = n7/7 + n6/2 + n5/2 – n3/6 + n/42
S (n7) = n8/8 + n7/2 + 7n6/12 – 7n4/24 + n2/12
S (n8) = n9/9 + n8/2 + 2n7/3 – 7n5/15 + 2n3/9 – n/30
S (n9) = n10/10 + n9/2 + 3n8/4 – 7n6/10 + n4/2 – n2/12
S (n10) = n11/11 + n10/2 + 5n9/9 – n7 + n5 – n3/2 + 5n/66
Потом Я. Бернулли указал общую формулу
S(nc) = nc+1/c+1 + 1/2*nc + 1/2*( )Anc-1 + 1/4*( )Bnc-3 + 1/6*( )Cnc-5 + 1/8*( )Dnc-7+ …
тут ( ), ( ) … – числа сочетаний; характеристики степени n убывают, крайний член в правой части содержит n либо n2. Числа A, B, C, D … – коэффициенты при n в выражениях S(n2), S(n4), S(n6), … Конкретно: А=1/6, В=-1/30, С=1/42, D=-1/30, …Бернулли определяет общее правило для вычисления этих чисел: сумма коэффициентов в выражениях S(n), S(n2), S(n3), … равна единице. к примеру, 1/9+1/2+2/3-7/15+2/9+D=1. Отсюда D=-1/30.
Я. Бернулли подчеркивает удобство таблицы фигурных чисел и заявляет, что с ее помощью в течение «половины четверти часа» отыскал сумму 10-х степеней первой тыщи натуральных чисел. Она оказалась равной
91 409 924 241 424 243 424 241 924 242 500.
II
Роль И. Бернулли как 1-го из создателей, распространителей и, безусловн, знатоков зарождавшегося тогда математического анализа отражает современная терминология: заглавие «интегральное исчисление» (от латинского integer — целый, откуда и старинное российское «целственный анализ») ввел И. Бернулли. Как понятно, Лейбниц предпочитал именовать интеграл «суммой». Это потом породило символ интеграла ∫, который представляет собой вытянутую буковку S— первую буковку латинского слова summa.
И. Бернулли занимался приложением рядов к интегрированию и на этом пути открыл общую формулу разложения в ряд интеграла от функции n(z) по степеням аргумента:
∫ n(z)dz = nz – z2/2 * dn/dz + z3/6 * d2n/dz2 – z4/24 * d3n/dz3 + …
В “Acta Eruditorium” за 1697 г. И. Бернулли поставил задачку о кривых, пересекающих некое плоское семейство однопараметрических линий под данным углом либо под углом, меняющимся по определенному закону. В первом случае линии движения именуются изогональными, а если угол прямой, то ортогональными. И. Бернулли указал на возможность внедрения приобретенных закономерностей в теории света Гюйгенса. Через год он показал, что задачка отыскания траекторий сводится к дифференциальному уравнению первого порядка.
Николай II Бернулли, отпрыск И. Бернулли, в 1720 г. определил задачку о обоюдных траекториях, т. е. о траекториях, относящихся к тому же семейству кривых, что и кривые данного семейства. Данной задачей занимался И. Бернулли. Он в 1727 г. в качестве семейства обоюдных траекторий именовал полукубические параболы y3 = ax2.
Лейбниц и И. Бернулли отыскали способ интегрирования оптимальных дробей, которые опосля выделения целой части они представляли в виде суммы простых дробей. Воплощение этого способа сделалось вероятным только тогда, когда сформировалось понятие логарифмической функции. В связи с интегрированием оптимальных дробей в анализ вошли всеохватывающие числа и появился спор о логарифмах отрицательных чисел.
В письмах Лейбницу 1702 г. И. Бернулли увидел, что оптимальные дроби должны встраиваться в оптимальных, логарифмических и радиальных функциях.
Представляет особенный Энтузиазм работа «Решение одной задачки интегрального исчисления», написанная в ”Memoires” Парижской академии за 1702 г. (1704) и в “Acta Eruditorium” за 1703 г., в какой И. Бернулли разглядел вариант реальных разных корней знаменателя рациональной дроби и в отличие от Лейбница, давшего готовые формулы, показал, как получать коэффициенты, сначала полагаемые неопределенными. тут же И. Бернулли увидел последующее принципиальное свойство. Подобно тому как дифференциал dz/(1-z2) при помощи подстановки z = (t-1)/(t+1) перебегает в логарифмический дифференциал dt/2t, так и дифференциал реального радиального сектора dz/(1 + z2) при помощи надуманной подстановки z = √-1(t-1)/(t+1) перебегает в «надуманный дифференциал» -dt/2√-1t. Не считая того, разумеется, что dz/(1+z2) = 0,5dz/1 + z√-1 + 0,5dz/1 – z√-1
т. е. дифференциал реального радиального сектора равен сумме дифференциалов надуманных логарифмов. Отсюда И. Бернулли сделал вывод, что надуманные логарифмы подменяют действительные радиальные секторы.
Соотношением dz/(1+z2) = -dt/2√-1t по существу была установлена связь меж функциями Arctg(z) и Ln t = ln (1 – z√-1)/(1 + z√-1). Но эту связь И. Бернулли не получил, потому что не стал интегрировать уравнение, а выполнил еще одну подстановку
t = (√-1 + √1/r – 1)/(√-1 – √1/r – 1), что отдало выражение дифференциала арксинуса реального аргумента через дифференциал надуманного логарифма.
Работа И. Бернулли, размещенная в “Acta Eruditorium” за 1712 г., содержала продолжение такого же исследования: в ней И. Бернулли проинтегрировал рациональную дробь с надуманным аргументом. Он решил дифференциальное уравнение
ndx/(x2 + 1) = dy/(y2 + 1), за ранее разложив дроби по обозначенному способу, и получил (x – √-1)n(y + √-1) = (x + √-1)n(y – √-1).
Продвижению вперед в применении надуманных чисел к анализу препятствовали неясности, связанные с понятием логарифма. Свидетельство этому — развернувшаяся меж Лейбницем и И. Бернулли дискуссия о природе логарифмов отрицательных чисел.
В 1712 г. Лейбниц выступил со статьей, где, обсуждая феномен Арно 1/-1 = -1/1, произнес, что отрицательным отношениям не соответствуют никакие логарифмы, так как положительным логарифмам соответствуют числа больше единицы, а отрицательным — правильные положительные дроби. Потому логарифм числа —1 не будет настоящим, он надуманный. И еще: если б этот логарифм был реальным, то его половина стала бы также реальной, т. е. реальным был бы логарифм надуманного числа √-1 а это ошибочно.
И. Бернулли возражал Лейбницу; он считал, что логарифмы отрицательных чисел действительны, и считал lg (-a) = lg а, потому что lg (-1) = 0. Он основывался на том, что из тождества d(-х)/-х=dх/х следует d lg (-х) = d lg х, т. е. lg (-x) = lg х. Приводились и остальные аргументы.
Перечислим некие личные результаты И. Бернулли. Он получил и опубликовал в 1701 г. разложения sin n a и cos n a по произведениям степеней sin n a и cos n a. Он 1-ый нашел и обосновал расходимость гармонического ряда. До сего времени в учебной литературе находит для себя пространство феномен И. Бернулли. Запишем таблицу
1/1*2 1/2*3 1/3*4 1/4*5…
1/2*3 1/3*4 1/4*5…
1/3*4 1/4*5…
…………………………….
Просуммируем по строчкам; найдем
S1 = 1/1*2 + 1/2*3 + 1/3*4 + 1/4*5+…= 1 – ½ + ½ – 1/3 + 1/3 – ¼ + … = 1,
S2 = ½ – 1/3 + 1/3 – ¼ +… = 1/2
S3 = 1/3 – ¼ + ¼ – 1/5 + … = 1/3
…………………………………….
Обозначим сумму строк буковкой S:
S=S1+S2+S3+…=1 + ½ + 1/3 + …
Просуммируем сейчас столбцы и сложим результаты; получим
s1=1/2, s2=1/3, s3=1/4, …; s1+s2+s3 + … =1/2+1/3+1/4+ … = S-1
Выходит феномен: S=S—1. Все разъясняется просто: мы оперируем с расходящимся гармоническим , не имеющим суммы.
Продолжим разговор о достижениях И. Бернулли. Он вослед за Я. Бернулли получил формулу для радиуса кривизны в дифференциалах абсциссы и ординаты, которая размещена в «Анализе нескончаемо малых» Лопиталя. И. Бернулли занимался исследованием параметров эволют, эвольвент, каустик, касательных, точек перегиба, огибающих, кривизны. Он открыл точку возврата второго рода, описанную Лопиталем. И. Бернулли выполнил почти все квадратуры, спрямления, кубатуры, в качестве приложения способов анализа решил мною геометрических и механических задач, в том числе задачку о парацентрической изохроне.
К середине 90-х годов XVII в., т. е. всего через 10 лет опосля возникновения основополагающего труда Лейбница, усилиями Лейбница и братьев Бернулли идеи дифференциального и интегрального исчислений достигнули такового развития, что возникли суждения о окончании анализа в ближнем будущем. Назрела необходимость собрать воедино и классифицировать разработанные способы с тем, чтоб ими мог воспользоваться наиболее широкий круг людей. Эту задачку искрометно выполнил И. Бернулли, написавший в 1691—1692 гг. «Лекции по исчислению дифференциалов» и «Математические лекции о способе интегралов и остальных вопросцах, написанные для маркиза Лопиталя».
Окончание лекций отдало возможность писать И. Бернулли в автобиографической заметке, что он «был первым, кто помыслил о изобретении способа для перехода от нескончаемо малых количеств к конечным, элементами которых эти нескончаемо малые сущность. Я именовал этот способ интегральным исчислением, не обнаружив наиболее пригодного слова».
Хотя И. Бернулли лекции и не издал, они были доступны французским математикам и сыграли важную роль в прогрессе анализа. Как уже говорилось, лекции и материалы, приобретенные Лопиталем в письмах И. Бернулли (они переписывались с 1692 г. в течение 10 лет), послужили Лопиталю основой при написании им «Анализа нескончаемо малых».
Лекции И. Бернулли, «Анализ» Лопиталя содержали маленькой набор главных аналитических понятий, иллюстрируемых чертежами, теорем и правил и огромное количество задач геометрического, механического и физического нрава.
Лекции по дифференциальному исчислению начинаются последующими постулатами:
«1. Величина, уменьшенная либо увеличенная на нескончаемо наименьшую величину, не миниатюризируется, не возрастает.
2. Всякая кривая линия состоит из нескончаемо почти всех прямых, которые сами нескончаемо малы.
3. Фигура, заключенная меж 2-мя ординатами, разностью абсцисс и нескончаемо малым кусочком хоть какой кривой, рассматривается как параллелограмм».
сходу же за вступлением И. Бернулли пишет: «Из предшествующего понятно, что dx есть дифференциал х, что хdх есть дифференциал ½*х2 либо ½*x2 плюс либо минус неизменная, x2dx — дифференциал 1/3*x3 плюс либо минус неизменная… также аdх — дифференциал ах и т. д., axdx – дифференциал ½*ax2 ах3dx— дифференциал ¼*ax4 и т. д.” Опосля этого дается общее правило: «ахp есть дифференциал количества axp+1/(p+1). Другими словами: ∫хpdx = хp+1/(р+1)*(+С). И. Бернулли применяет это правило к случаю P=-1 и получает ∫ dx/x = ∞. Но потом он исправляет ошибку.
Потом рассматриваются некие варианты общей формулы: случаи, когда можно выделить дифференциал подкоренного выражения, и т. д.
2-ая лекция посвящена вычислению площадей. И в этом вопросце И. Бернулли развивал идеи Лейбница и писал: « площади разглядывают как разложенные на части, каждую из которых можно считать дифференциалом площади. Если имеют интеграл этого дифференциала, т. е. сумму этих частей, то отсюда будет известна и разыскиваемая квадратура».
Опосля обсуждения разных методов разбиения фигуры И. Бернулли делает заключение: когда частичные площадки ограничены ординатами и кривой, дифференциал каждой из их будет уdх. Если кривая задается, то у выражается через х полностью точно, и уdх будет «на сто процентов выражаться через х». Он приводит пример: дана парабола у2=ах; дифференциал площади будет √ах dх, его интеграл 2/3х√ах, либо 2/3xу. С необыкновенной простотой И. Бернулли отыскал итог, считающийся важным достижением геометрии старых, состоящий в том, что площадь сектора параболы равна 2/3 площади соответственного прямоугольника ху.
Содержание последующих лекций очень многообразно: квадратуры площадей, кривых, «оборотные задачки», соприкасающиеся кривые и эволюты, каустики; завершают книжку 5 лекций, посвященных решению физико-механических задач, в том числе задачки и цепной полосы — одной из первых задач механики нити. Поражает в тех и остальных лекциях, не считая содержания, высокое методическое мастерство. Все в их все как у опытнейшего лектора, хотя ему было всего 24 года. И лекций по анализу нескончаемо малых до него не читал никто.
Не достаточно займет места изложение обширно известного правила Лопиталя, но следует его выделить посреди общего рассмотрения творчества И. Бернулли. В письме 22 июля 1694 г. И. Бернулли дал ответ Лопиталю на вопросец о том, как надо поступать, когда нужно отыскать
Лопиталь определяет задачку так: «.Пусть величина ординаты у кривой АМD (АР=х, РМ=у, АВ=а) выражается дробью, числитель и знаменатель которой обращаются в нуль при х=а, т. е. когда точка Р совпадает с данной точкой В. Спрашивается, какой обязана быть при атом величина ординаты ВD».
Решение задачки смотрится так. На общей «оси» строятся кривые АNВ и СОВ, при этом ордината РN заходит в числитель, а РО — в знаменатель дроби для всех РМ, так что РМ=АМ•РN/РО.
Обе кривые пересекаются в точке В, так как, по предположению,
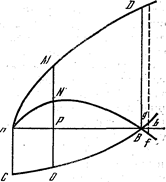
величины РN и РО обращаются в нуль, когда точка Р совпадает с В. Потом вводится ордината bd, близкая к ВD и пересекающая кривые в точках f и g. Для нее будет Bd=AB*bf/bg, что не различается от ВD в силу 1-го из главных допущений, выдвинутых создателем, о том, что если имеются две величины, отличающиеся друг от друга на нескончаемо малую, то можно брать одну из их заместо иной. Как следует, нужно отыскать отношение bg к bf.
Когда АР обращается в АВ, обе ординаты РN и РО обращаются в нуль, «а когда АР обращается в Аb, ординаты обращаются в bf и bg». означает, ординаты bf и bg являются дифференциалами кривых АNВ и СОВ в точках В и b. Потому для нахождения искомого значения bd иди ВD необходимо дифференциал числителя поделить на дифференциал знаменателя, положив х=а=Аb либо АВ, «что и требовалось отыскать»,— заключает Лопиталь.
В последующем параграфе правило применяется к нахождению предельного значения
y = (√2a3x – x4 – a√a2x)/(a – √ax3) при х=а.
Лопиталь пишет: необходимо дифференциал числителя поделить на дифференциал знаменателя, положив х=а. Получим число 16а/9 «для разыскиваемой величины ВD».
В августе 1704 г., скоро опосля погибели Лопиталя, И. Бернулли выступил с первым печатным заявлением, в каком предъявил претензии на описанные в «Анализе» способы. Это была заметка «Усовершенствование моего размещенного в “Analyse des infiniment petits” § 163 способа для определения значения дроби, числитель и знаменатель которой время от времени исчезают». тут И. Бернулли поведал, что правило он сказал в письме Лопиталю лет 10 вспять, также решил пример, помещенный в § 164, который французские арифметики и Лопиталь решить не могли. В той же заметке И. Бернулли, «движимый любовью к правде», отметил, что время от времени однократное применение правила к цели не приводит, выходит снова неопределенность вида 0/0, потому его приходится использовать еще один либо пару раз.
Сразу с развитием дифференциального и интегрального исчислений шла разработка способов решения дифференциальных уравнений. В интегрировании уравнений первого порядка были достигнуты значимые успехи. В «Математических лекциях о способе интегралов и о остальных вопросцах, написанных для маркиза Лопиталя» принято решение однородное уравнение dy/dx=f(y/x) подстановкой у=хt. Там же изложен способ приведения к однородному уравнения dy/dx=f((ax+by+c/(a1x + b1y + c1)) подстановками x = ξ + h, у = η +h; при всем этом не упомянут вариант ab1-a1b=0. В «Лекциях» И. Бернулли применил интегрирующий множитель к уравнению ахdу—уdх=0. Он помножил члены уравнения на уa-1/x2 и получил d(ya/x;)=0, откуда уa=bх. Конкретное разделение переменных в этом уравнении И. Бернулли не выполнил, потому что считал, что в согласовании с формулой ∫хndх=хп+1/(n+1) будет ∫dx/x=∞. (Как понятно, потом он выражал этот интеграл через ln x.)
В письме Лейбницу 4 сентября 1696 г. И. Бернулли показал, что «уравнение Бернулли» dy/dx=р(х)у+q(х)уn сводится подменой у1-n=z к линейному. Из письма Лейбницу в том же году следует, что И. Бернулли проинтегрировал уравнение у=хφ(dу/dх)+ψ(dу/dх), называемое сейчас уравнением Лагранжа. Около 1700 г. И. Бернулли применил интегрирующий множитель xk для поочередного снижения порядка уравнения Эйлера
а0хndпу/dхn+а1хп-1dп-1у/dхn-1+ … +аn-1хdу/dх+аny=0.
Кроме этого И. Бернулли занимался еще уравнением Риккати и задачей о колебании струны.
Статья И. Бернулли «Общий метод построения всех дифференциальных уравнений первого порядка» содержит идею способа изоклин, используемого при графическом решении уравнений первого порядка. Существо вопросца состоит в последующем. Общему решению у=f(x; С) дифференциального уравнения первого порядка у’=f(х; у) на плоскости соответствует семейство интегральных кривых. Само уравнение описывает в каждой точке плоскости означает, дифференциальное уравнение задает поле уравнений, а задачка нахождения общего решения уравнения состоит в отыскании кривых, для которых направления касательных совпадают с направлениями поля.
III
3-ий превосходный представитель рода Бернулли, Даниил, занимает посреди Бернулли и в науке особенное пространство. Изюминка эта разъясняется, во-1-х, разносторонностью его научных интересов и значительностью приобретенных им результатов фактически во всех областях четкого естествознания собственного времени, во-2-х, прикладной направленностью исследовательских работ. В книжках, в какой-нибудь мере связанных с историей науки, Даниила Бернулли именуют по-разному: физиологом, астрологом, физиком, математиком, механиком, гидродинамиком. И не без основания: Д. Бернулли вкупе с Л. Эйлером, И. Бернулли, Ж. Д’Аламбером, Ж. Лагранжем и иными выдающимися математиками и механиками XVIII в. создавал базы традиционной науки.
В очерке о роде Бернулли говорилось, что в 1723 г. Д. Бернулли отправился в Венецию для занятия медициной под управлением итальянского доктора П. А. Микелотти. За два года до приезда Д. Бернулли в Венеции была размещена «физико-механико-медицинская» диссертация Микелотти «О разделении жидкостей в теле звериного», в какой рассматривались вопросцы гидродинамики {живых} организмов. Она вышла в одном переплете со вторым изданием мед диссертации И. Бернулли «О движении мускулов», что свидетельствовало о научном авторитете Бернулли посреди итальянских ученых и благоприятствовало деятель Д, Бернулли в Венеции.
При помощи «1-го авторитетного венецианца» Д. Бернулли в 1724 г. издал «Математические упражнения» («Даниила Бернулли из Базеля, отпрыска Иоганна, некие математические упражнения»), направленные в защиту мыслях отца и дяди от нападок неких итальянских ученых. Книжка представляет вроде бы обзор научной деятель создателя за прошлые годы и содержит почти все идеи, развитые им потом. Через год некие результаты были размещены в «Acta Eruditorium» и стали достоянием наиболее широкого круга ученых.
«Математические упражнения» состоят из 4 разделов: три посвящены арифметике, один (2-ой) — приложениям арифметики к гидравлике и медицине. В части книжки, связанной с арифметикой, Бернулли полимезирует с итальянскими математиками (Д. Ризетти, Д. Риккати и др.) по разрабатываемой в то время незапятанной арифметике. Тут содержится много ссылок на работы, помещенные в различное время в «Acta Eruditorium»; это служит свидетельством того, что создатель был в курсе новейших открытий. Более значима часть книжки, посвященная исследованию дифференциального уравнения Риккати.
Развитие арифметики в первой половине XVIII в. характеризовалось тем, что вместе с детализированным рассмотрением разных классов функций наблюдалось предстоящее исследование дифференциальных уравнений и применение их к задачкам механики, дифференциальной геометрии, вариационного исчисления. Уравнения встраивались как в конечном виде, так и при помощи рядов.
Ко времени опубликования «Математических упражнений» в работах Лейбница, Я. и И. Бернулли были найдены методы интегрирования однородных и линейных уравнений первого порядка, также уравнений Я. Бернулли.
y’=f(х; у), в каком правая часть является функцией дела у/х. В 1693 г. Лейбниц отыскал способ сведения таковых уравнений к уравнениям с разделяющимися переменными подстановкой у=их.
Линейное уравнение первого порядка имеет вид у’+Р(х)у=Q(х).
способ решения таковых уравнений, когда функция у отыскивается в виде произведения 2-ух новейших функций (у=иу), был разработан приблизительно в то же время и также Лейбницем. Уравнение вида
y’+Р(х)у=Q(х)уп предложил Я. Бернулли. Оно в 1696—1697 гг. было принято решение этим же способом, что и линейное, Лейбницем, Я. и И. Бернулли; не считая того, Лейбниц и И. Бернулли проявили, что оно сводится к линейному подстановкой y1-n=z
К неким уравнениям применялся также интегрирующий множитель. Я. Бернулли предложил прием снижения порядка к уравнению второго порядка, не содержащему очевидно одной из переменных, подменой y’=p. Работа Я. Бернулли увидела свет позже, опосля того как Риккати в 1715 г. опубликовал свое исследование о том же способе.
В 1694 г. в «Асtа Eruditorium» И. Бернулли расположил маленькую статью, в какой упоминалось уравнение тина Риккати. Он писал: «Я еще не узнал, можно ли разрешить дифференциальное уравнение х2dх + у2dх = d2у». Опосля данной для нас публикации уравнением y’=у2+х2
заинтересовался Я. Бернулли, о чем свидетельствуют его письма Лейбницу в 1697—1704 гг. «Я бы желал дальше от тебя выяснить, пробовал ли ты изучить dу=у2dх+х2dх,— писал Я. Бернулли Лейбницу 27 января 1697г.— Я делал огромное количество попыток, но решение данной для нас задачки повсевременно ускользало от меня». «К слову, я вспоминаю другое уравнение dу=у2dх+х2dх,— писал он Лейбницу 15 ноября 1702 г.,— в каком мне не удалось поделить переменные так, чтоб уравнение осталось просто дифференциальным; но я поделил их сведением к последующему дифференциальному уравнению: d2у:у=-х2dx2».
Хотя Я. Бернулли не удалось решить уравнение в конечном виде, Энтузиазм к нему у математиков утих. Только в 1724 г. граф Джакопо Риккати в Дополнении VIII к «Асtа Eruditorium» поставил задачку: для уравнения у’=ахп+bу2 (а и b — неизменные) отыскать значения п, при которых оно допускает разделение переменных. Ею занялись Иоганн I, Николай I, Николай II и Даниил Бернулли, но, не считая Даниила, существенных результатов никто не получил.
Д. Риккати свое решение в упомянутом дополнении выразил в виде анаграммы.
В том же выпуске «АсtaEruditorum» была помещена заметка Д. Бернулли, в какой он написал, что уравнение ахndх+ииdх=bdи считается неразрешимым.
Бернулли приступил к исследованию уравнения и скоро опубликовал свои результаты в «Математических упражнениях». Он установил, что уравнение Риккати допускает интегрирование в конечном виде в вариантах n= -4k/(2k±1) (k—целое число).
Вариант п=—2 разглядел Эйлер. В 1841 г. Лиувилль обосновал, что в вариантах, хороших от обозначенных Д. Бернулли и Эйлером, решение уравнения Риккати не сводится к квадратурам и не быть может выражено при помощи конечного числа простых функций. Уравнение
у’+а(х)y2+b(x)y+c(x)=0
сейчас именуют обобщенным уравнением Риккати. Его изучил Эйлер и установил, что если понятно одно личное решение у1(х) уравнения, то подстановка y=y1 (х)+1/и{х) приводит его к линейному. Если же известны два личных решения y1(x) и у2(x), то общий интеграл уравнения находится одной квадратурой.
Энтузиазм к уравнению Риккати разъясняется тем, что оно встречается при решении неких задач механики; не считая того, к нему можно свести хоть какое линейное уравнение второго порядка.
Интересы Д. Бернулли были многообразны. И скоро он заинтересовался старой неразрешимой задачей квадратуры круга просуществовавшей почти все века, будоража мозги математиков всех времен. Гиппократ Хиосский (V в. до н. э.) пробовал совладать с квадратурой круга с помощью квадрируемых фигур, ограниченных дугами 2-ух окружностей, нареченных гиппократовыми луночками. Такую луночку можно, к примеру, выстроить последующим образом: возьмем четверть круга радиуса r и на хорде АС, соединяющей концы радиусов ОА и ОС, опишем как на поперечнике внешнюю по отношению к четверти круга полуокружность.
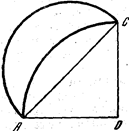
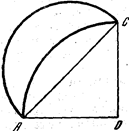
Тогда АС=r√2 и площадь четверти большего круга будет таковой же, как площадь наименьшего полукруга, т. е. πr2/4.
Пусть S—площадь луночки, S1, S2, S3, S4, —площади соответственно наименьшего полукруга, сектора АС, четверти большего круга, треугольника ОАС. Найдем
S=S1-S2, S2=S3—S4,
потому
S= πr2/4- (πr2/4-S4) =S4.
Итак, S=r2/2. Это означает — луночка квадрируема.
Гиппократ получил три квадрируемые луночки. Д. Бернулли в «Математических упражнениях» указал условие, которому должны удовлетворять алгебраически квадрируемые луночки, и привел уравнение, дающее четвертую квадрируемую луночку.
Но луночки Гиппократа задачку о квадратуре круга вперед к решению не продвинули: в 30—40-х годах XX в. И. Г. Чеботаревым и А. В. Дородновьш подтверждено, что существует 5 видов квадрируемых луночек, но они не квадрируемы вкупе с кругом.
2-ая часть «Математических упражнений», посвященная вопросцам механики, по размеру составляет практически половину книжки.
В 1725 г. Д. Бернулли вкупе с И. Бернулли получил первую премию на объявленном Парижской академией первом конкурсе на тему «О средствах сохранять равномерность водяных либо песочных часов на море». Считается, что этот фуррор исследования по прикладной механике обусловил неизменный Энтузиазм Д. Бернулли к практическим задачкам. И 5 июля 1725 г. был подписан договор, по которому Д. Бернулли предоставлялось пространство доктора физиологии Петербургской академии с жалованьем 800 рублей в год; 27 октября 1725 г. он вкупе с братом Николаем II Бернулли, получившим профессуру по кафедре арифметики с окладом 1000 рублей (самым высочайшим из всех платившихся академикам—составлял 4% от суммы, отпущенной Петром I на компанию академии), прибыл в Петербург. В духе механистических мнений XVII—XVIII вв. Д. Бернулли на кафедре анатомии и физиологии намеревался при помощи механикоматиматических способов учить потаенны жив природы. Он желал открыть «новейшую эру в физиологии » (из письма Гольдбаху от 17 июня 1730 г.). Вышло же совершенно другое: открытия Д. Бернулли легли в базу гидродинамики, гидравлики, физиологии ; они используются в геологии, при исследовании динамики звёзд, в остальных областях четкого естествознания.
Уже упоминалось, что 4 декабря 1725 г. на собрании академиков Д. Бернулли сделал сообщение «Возражение Питкарну против его теории о выделении соков в теле звериного». На эту же тему через две недельки он сделал 2-ой доклад. Потом тема исследовательских работ Д. Бернулли поменялась: он стал учить движение мускул человека и звериных.
В связи с сиим встали чисто механические задачки, определившие сообщения Д. Бернулли: «О сложении и разложении сил» (1 февраля 1726 г.), «Геометрические подтверждения к рассуждению о сложении сил» (14 июня 1726 г.) и 1-ые публикации в первом томе «Объяснений» Петербургской академии (1728) — «Исследование принципов механики и геометрические подтверждения относительно сложения и разложения сил», «Опыт новейшей теории движения мускулов». В этих работах Д. Бернулли развивал идеи, изложенные И. Бернулли в диссертации «О движении мускулов».
погибель Николая Бернулли омрачила 1-ые годы жизни Д. Бернулли в Петербурге. На заседании Академии 1 августа 1726 г. императрица Екатерина I выразила Д. Бернулли свое соболезнование.
Скоро погибла Екатерина I; пришедший на престол Петр II переехал в Москву, куда отправился и президент академии Блюментрост. Фактическим управляющим академии стал прошлый библиотекарь Петра I И. Д. Шумахер, и это не благоприятствовало работе академии.
По инициативе и настоянию Д. Бернулли в 1727 г. в Петербург был приглашен величавый Л. Эйлер. Он занял пространство адъюнкта на кафедре анатомии и физиологии и подготовил трактат «Базы движения крови по артериям». Но интересы Эйлера лежали в другом русле: его занимало как развитие самой арифметики, так и внедрения ее к механике, физике, астрономии, и в 1731 г. он перебежал на кафедру физики, в 1733 г.—на кафедру арифметики.
По распоряжению президента Академии Блюментроста любой доктор должен был написать какой-нибудь трактат.
В 1732 г. Бернулли опубликовал работу «Замечания о рекуррентных последовательностях», где выложил способ решения алгебраических уравнений, не нуждающийся в подготовительном определении границ, меж которыми лежат положительные и отрицательные корешки.
слово рекуррентный значит возвратимый. Рекуррентными формулами в арифметике именуются такие, в каких какая-либо следующая величина рассчитывается через прошлые. Таковы же и последовательности. Конкретно: последовательность именуется рекуррентной, если ее n-й член выражается через некие прошлые линейно: an=a1an-1+aan-2+…+akan-k. К рекуррентным последовательностям относятся, к примеру, известные геометрическая и арифметическая прогрессии, для которых an =an-1q, an=an-1q+d, где q — знаменатель геометрической прогрессии, d — разность арифметической. Могут быть и рекуррентные степенные ряды, т. е. ряды, коэффициенты которых образуют рекуррентные последовательности. Такие ряды разглядывал до Д. Бернулли А. Муавр в «Philosophical Transactions» за 1722 г. А. Муавр пришел к ним при решении одной вероятностной задачки.
Д. Бернулли предложил собственный способ решения уравнений без обоснования, которое дано было потом Л. Эйлером. Разглядим уравнение
a0xn +a1xn-1+a2xn-2+…+an=0 (1)
и представим, что оно имеет действительные разные корешки x1, x2,…, xn. Составим конечно-разностное уравнение
a0yn+i+a1yn+i+…+anyi=0 (i = 0, 1, 2,…), (2)
в которое войдут коэффициенты аk (k=0; 1; 2;…) уравнения (1). Уравнение (2) представляет собой рекуррентное соотношение для последовательности
y0,y1,y2,…уi,…. (3)
Эта последовательность описывает решение конечноразностного уравнения (2). Для нахождения решения у1 необходимо задать п исходных значений y0, y1,…, yn-1;
другие уn, yn+1,…можно найти из уравнения (2).
В теории конечных разностей доказывается, что если корешки x1, x2,…,xn уравнения (1) различны, то решения, конечно-разностного уравнения (2) имеют вид
yi=C1x1i+C2x2i+…+Cnxni (i=0, 1, 2,…), (4)
где C1, С2,…, Сn — произвольные неизменные, которые можно найти из исходных критерий:
y0=C1+C2+…+Cn, (5)
y1=C1x1+C2x2+…+Cnxn,
yn-1=C1x1n-1C2x2n-2+…+Cnxnn-1.
Докажем аксиому: если алгебраическое уравнение (1) имеет единственный больший по модулю корень x1, то отношение 2-ух поочередных членов yi+1 и y1, решения конечно-разностного, уравнения (2) стремится при i®¥ к лимиту, равному x1
yi+1
lim ——— = x1.
i®¥ yi
Представим, что |x1|>|x2|≥…≥|xn|. Если корешки хk (k=1, 2,…, n) различны, то из (4) получим
yi=x1i[C1+C2(x2/x1)i+…+Cn(xn/x1)i],
yi+1=x1i+1[C1+C2(x2/x1)i+1+…+Cn(xn/x1)i+1],
Найдемтеперь
yi+1/yi=x1 (C1+C2(x2/x1)i+…+Cn(xn/x1)i)/( C1+C2(x2/x1)i+1+…+Cn(xn/x1)i+1)
Пусть С=0. Перейдем в крайнем равенстве к лимиту при i®¥ и учтем, что (x2/x1)i→0; (х3 /х2)i→0;…;(x4/x1)i→0. Получим то, что и требовалось обосновать.
Быть может так, что C1=0, но С2≠0. Тогда обозначенный предел будет равен другому, большему по абсолютной величине, корню уравнения.
В случае, когда отношение yi+1/yi, колеблется и не стремится к определенному лимиту, предполагается, что у уравнения есть самые большие по модулю всеохватывающие корешки.
Создадим в уравнении подмену x=1/z. Опосля этого по способу Бернулли найдется меньший по модулю хороший от нуля корень.
Реализация способа Бернулли делается так. Поначалу задаются произвольные числа y0; y1,…,yn-1, потом по формуле
yn+1=-(anyi+an-1yi-1+…+a1yn+i-1)/a0 (i=0, 1, 2, …)
находятся числа уn, yn+1, yn+2,… и дела yn/yn-1, yn+1/yn,… Если отношение yn+1/ yn+i-1 при возрастании i стремится к некому числу, то его принимают за больший по модулю корень уравнения (1). Если же отношение с ростом i к лимиту не стремится, то уравнение может иметь несколько больших по модулю корней либо же это будет свидетельством того, что для избранных y0, y1,…
Исходные значения y0, y1,…, yn-1 выбираются произвольно; обычно считают y0=y1=…=yn-2=0,
yn-1=1. способ Бернулли используют также для нахождения всеохватывающих корней уравнения (1).
В публикации 1738 г. Д. Бернулли распространил способ рекуррентных последовательностей на вариант рядов.
Как вдруг возникли ряды? Дифференциальное и интегральное исчисления появились в связи с необходимостью решать определенные механические и геометрические задачки, не поддававшиеся средневековой и древней арифметике. А ряды? Они на 1-ый взор кажутся очень искусственными. Но это глубочайшее заблуждение. Ряды появились сразу с дифференциальным и интегральным исчислениями, и теория их строилась Ньютоном, Лейбницем, представителями семьи Бернулли и следующими математиками. И при исследовании их деятель рельефно выступают ее проблематика и методология.
С рядами дело обстояло так же естественно, как и с иными важными разделами арифметики, получившими бурное развитие в XVIII в.: они применялись там, где остальные средства исследования отказывали. Степенные ряды давали возможность приближенно решать уравнения, вычислять значения функций, вычислять интегралы, не выражающиеся через конечное число простых функций, решать дифференциальные уравнения, не интегрируемые в конечном виде.
В 1732 г. Парижской академией был объявлен конкурс с двойной премией на тему «О обоюдном наклонении планет». Премию получили Д. и И. Бернулли. Премированы также сочинения Д. Бернулли: «О наилучшем методе устройства якорей» (1738), «О морском приливе и отливе» (1740), «О лучшем методе устройства магнитных стрелок наклонения» (1743), «О наилучшем методе определения времени в море» (1745-1746), «Теория магнита» (1742, 1744, 1746), «О теории течений и о наилучшем методе их следить» (1751 двойная премия), «О более удачном методе подмены деяния ветра на огромных судах» (1753), «О лучшем методе уменьшения боковой и килевой качки судна» (1757).
У семьи Бернулли есть также много остальных открытий в области высшей арифметики и физики. Вот несколько примеров таковых открытий:
БЕРНУЛЛИ СХЕМА (назв. по имени Я. Бернулли), одна из главных математических моделей для описания независящих повторений опытов, применяемых в теории вероятностей. Бернулли схема подразумевает, что имеется некий опыт Х и связанное с ним случайное событие А (обычный пример: S— бросание монеты, А – выпадение герба). Создают n независящих повторений S. При любом осуществлении S событие А может наступить с вероятностью р (тут р=1/2), либо наступить беда с вероятностью g=1-p. Таковым образом схема Бернулли определяется 2-мя параметрами: п и р.
БЕРНУЛЛИ ТЕОРЕМА, одна из важных теорем теории вероятностей; является простым случаем т. н. закона огромных чисел. Бернулли аксиома была в первый раз размещена в труде Я. Бернулли «Искусство догадок», изданном в 1713. 1-ые ее подтверждения добивались сложных математических средств, только в сер. 19 в. П. Л. Чебышев нашёл необыкновенно роскошное и короткое её подтверждение. Четкая формулировка аксиомы Бернулли такая: если при любом из п независящих испытаний возможность некого действия равна р, то возможность того, что частота т/п возникновения действия удовлетворяет неравенству |т/п—р|<ε (ε—произвольно маленькое положительное число), становится сколь угодно близкой к единице при довольно большенном числе п испытаний. Из подтверждения Чебышева вытекает обычная численная оценка данной для нас вероятности:
Р т/п—р>1—р(1—р)/пε2. В. И. Битюцков.
БЕРНУЛЛИ УРАВНЕНИЕ, дифференциальное уравнение 1-го порядка вида:
dy/dx + Py = Qya, где Р, Q — данные непрерывные функции от х, а — неизменное число. Введением новейшей функции z=y1-a. Уравнение Бернулли сводится к линейному дифференциальному
уравнению относительно z. Уравнение Бернулли было рассмотрено Я. Бернулли в 1695, способ решения размещен И. Бернулли в 1697 г.
БЕРНУЛЛИ УРАВНЕНИЕ, основное уравнение гидродинамики, связывающее (для установившегося течения) скорость текущей воды v, давление в ней р и высоту h расположения малого объёма воды над плоскостью отсчёта. Уравнение Бернулли было выведено Д. Бернулли в 1738 г. для струйки безупречной несжимаемой воды неизменной плотности ρ, находящейся под действием лишь сил тяжести. В этом случае уравнение Бернулли воспринимает вид:
v2/2+p/ρ + gh = const, где g – убыстрение силы тяжести. Если это уравнение помножить на ρ, то 1-й член будет представлять собой кинетическую энергию единицы размера воды, а остальные два члена – его потенциальную энергию. Уравнение Бернулли в таковой форме выражает законсохранения энергии.
Фамилия Бернулли мне встречалась весьма нередко, но до некого времени я не знал, что она принадлежит ряду ученых – родственников. Я думаю, почти все даже и не слышали данной для нас фамилии либо не догадываются, что Бернулли были теми людьми, о которых молвят, что они предназначили себя на сто процентов науке.
Броско не то, что это семейство сделало ряд важных открытий в различных областях науки, а то, что они, кроме лишь неких членов семьи, были как-либо соединены с наукой, а именно с арифметикой. недозволено ассоциировать «умных» представителей данной для нас фамилии с иными величавыми учеными, но они, пожалуй, были самыми превосходными учеными собственного времени. Почти все их открытия даже на данный момент кажутся нам мистическими, недоказуемыми, да и как все превосходное – ординарными.
Я не понимаю, что мне в дальнейшем понадобится из того, что я тут выложил, но я буквально понимаю, что не встречу и не услышу о иной таковой семье, подарившей миру столько гениев.
Перечень литературы
Н. Я. Виленкин «Величавые арифметики Бернулли»
«Большая Русская Энциклопедия» (в 30 томах). Гл. редактор А. М. Прохоров. 3-е издание М.. «Русская Энциклопедия» 1970 г.
« Энциклопедический словарь молодого математика»
«Справочник по простой арифметике» М. Я. Выгодский
]]>