Учебная работа. Курсовая работа: Решение систем дифференциальных уравнений методом Рунге — Кутты 4 порядка
ы
4 порядка
Курсовая работа по дисциплине : Математические способы и модели
в расчетах на ЭВМ
Выполнил: студент гр. ХТ-96 Кузнецов М.В.
Министерство образования Украины
Донецкий муниципальный технический институт
Кафедра хим технологии горючего
г. Донецк 1998 год
Введение
Простые дифференциальные уравнения (ОДУ) обширно употребляются для математического моделирования действий и явлений в разных областях науки и техники. Переходные процессы в радиотехнике, кинетика хим реакций, динамика био популяций, движение галлактических объектов, модели экономического развития исследуются при помощи ОДУ.
В дифференциальное уравнение n-го порядка в качестве неведомых величин входят функция y(x) и ее 1-ые n производных по аргументу x
j( x, y, y1
, … y(n)
)=0. 1.1
Из теории ОДУ понятно, что уравнение (1.1) эквивалентно системе n уравнений первого порядка
jk
(x, y1,
y1
’
,y2
,y2
’
, … ,yn
,yn
’
)=0. 1.2
где k=1, … , n.
Уравнение (1.1) и эквивалентная ему система (1.2) имеют нескончаемое огромное количество решений. Единственные решения выделяют при помощи доп критерий, которым должны удовлетворять разыскиваемые решения. Зависимо от вида таковых критерий разглядывают три типа задач, для которых подтверждено существование и единственность решений.
1-ый тип – это задачки Коши, либо задачки с исходными критериями. Для таковых задач не считая начального уравнения (1.1) в некой точке xo должны быть заданы исходные условия, т.е. значения функции y(x) и ее производных
y(x0
)=y0
’
, y’
(x0
)=y10
, … ,y(n-1)
(x0
)=yn-1
,0
.
Для системы ОДУ типа (1.2) исходные условия задаются в виде
y1
(x0
)=y10
,y2
(x0
)=y20
, … , yn
(x0
)=yn0
. 1.3
Ко второму типу задач относятся так именуемые граничные, либо краевые задачки, в каких доп условия задаются в виде многофункциональных соотношений меж разыскиваемыми решениями. количество критерий обязано совпадать с порядком n уравнения либо системы. Если решение задачки определяется в интервале x є [x0
,xk
], то такие условия могут быть заданы как на границах, так и снутри интервала. Малый порядок ОДУ, для которых быть может сформулирована граничная задачка, равен двум.
3-ий тип задач для ОДУ – это задачки на собственные значения. Такие задачки различаются тем, что не считая разыскиваемых функций y(x) и их производных в уравнения входят добавочно m неведомых характеристик l1,l2,¼, хm, которые именуются своими значениями. Для единственности решения на интервале [x0,xk] нужно задать m+n граничных критерий. В качестве примера можно именовать задачки определения собственных частот, коэффициентов диссипации, структуры электромагнитных полей и механических напряжений в колебательных системах, задачки нахождения фазовых коэффициентов, коэффициентов затухания, распределения напряженностей полей волновых действий и т.д.
К численному решению ОДУ приходится обращаться, когда не удается выстроить аналитическое решение задачки через известные функции. Хотя для неких задач численные способы оказываются наиболее действенными даже при наличии аналитических решений.
Большая часть способов решения ОДУ основано на задачке Коши, методы и программки для которой рассматриваются в предстоящем.
1. Постановка задачки
Почти все процессы хим технологии описываются СДУ — начиная от кинетических исследовательских работ и заканчивая хим технологическими действиями. В базу математических методов описания действий положены СДУ и СЛАУ. Эти уравнения обрисовывают вещественные и термо балансы объектов хим технологии, а так же структуры потоков технических веществ в этих аппаратах.
Для получения, распределения технологических характеристик во времени и в пространстве (в границах объекта), нужно произвести СДУ способом, которых отдал бы высшую точность решения при минималььных издержек времени на решение, поэтому что ЭВМ обязана работать в режиме настоящего времени и успевать за ходом технологического процесса. Если время на решение задачки огромное, то управляющее действие, выработанное на ЭВМ может привести к отрицательным действиям. Способов решения существует весьма много. В данной работе будет рассмотрен способ решения СДУ способом Рунге-Кутта 4 порядка.
Для удобства работы на ЭВМ , нужно данную кинетическую схему конвертировать в удачный для работы на компе вид. Для этого нужно кинетическую схему процесса представить в виде уравнений. При рассмотрении кинетической схемы процесса нужно учесть коэффициенты скоростей реакций. Но, потому что процесс протекает при изотермических критериях, коэффициенты скоростей реакций можно считать за константы скоростей хим реакции. Из приведенной ниже схемы мы можем составить ряд дифференциальных уравнений, учитывающих изотермичность процесса.
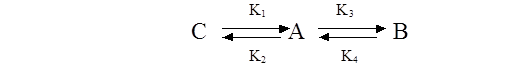
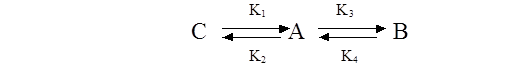
Потому что коэффициенты K1,K2,K3,K4 являются константами, то можно уравнение записать в следущем виде.
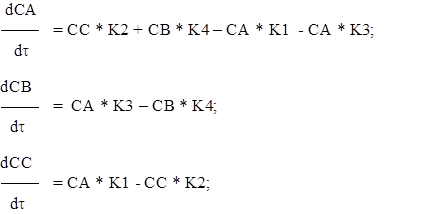
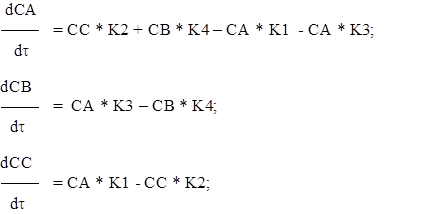
Для преобразования данных дифференциальных уравнений для использования их в расчетах термических и кинетических схем способами Рунге-Кутты нужно подставлять заместо производных значений концентраций, значения концентраций данных сначала процесса. Это обосновано тем, что способ Рунге-Кутты 4-ого порядка, который будет применен для расчета кинетической схемы процесса. Потому что этот способ просит сведений лишь о одной точке и значений функции.
2. Сущность способа
Разбор и рассмотрение способов, используемых на практике для решения дифференциальных уравнений, мы начнем с их широкой группы, известной под общим заглавием способов Рунге-Кутта.
способы Рунге-Кутта владеют последующими качествами:
1
Эти способы являются одноступенчатыми: чтоб отыскать уm+1
2
3.
.
Разглядим поначалу геометрическое построение и выведем некие формулы на базе геометрических аналогий. Опосля этого мы подтвердим приобретенные результаты аналитически.
Представим, нам известна точка xm,ym на разыскиваемой кривой. Тогда мы можем провести прямую линию с тангенсом угла наклона у¢m
=f(xm
,ym
), которая пройдет через точку xm
,ym
. Это построение показано на рис.1, где кривая представляет собой четкое, но естественно неведомое решение уравнения, а ровная линия L1 построена так, как это лишь что описано.
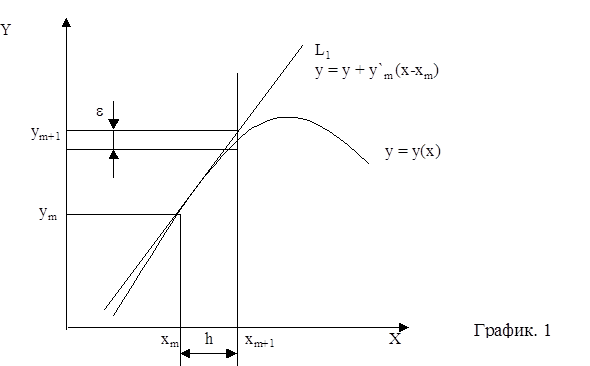
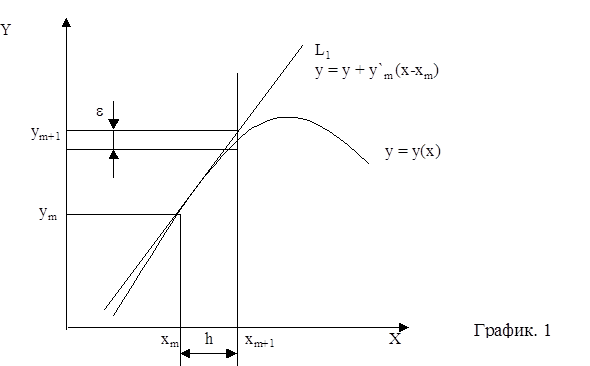
Тогда последующей точкой решения можно считать ту, где ровная L1
пересечет ординату, проведенную через точку x=xm+1
=xm
+h.
Уравнение прямой L1
смотрится так: y=ym
+y¢m
(x-xm
) потому что y¢=f(xm
,ym
) и не считая того, xm+1
=xm
+h тогда уравнение воспримет вид
ym+1
=ym
+h*f(xm
,ym
) 1.1
Ошибка при x=xm+1
показана в виде отрезка е. Разумеется, отысканное таковым образом приближенное
Заметим, что хотя точка на графике 1была показана на кривой, в реальности ym
является приближенным значением и не лежит буквально на кривой.
Формула 1.1 обрисовывает способ Эйлера, один из самых старенькых и обширно узнаваемых способов численного интегрирования дифференциальных уравнений. Отметим, что способ Эйлера является одним из способов Рунге-Кутта первого порядка.
Разглядим исправленный способ Эйлера и модификационный способ Эйлера.В исправленном способе Эйлера мы находим средний тангенс угла наклона касательной для 2-ух точек: xm
,ym
и xm
+h,ym
+hy¢m
. Крайняя точка есть та, которая в способе Эйлера обозначалась xm+1
,ym+1
. Геометрический процесс нахождения точки xm+1
,ym+1
можно проследить по рис.2. При помощи способа Эйлера находится точка xm
+h,ym
+hy¢m
, лежащая на прямой L1
. В данной точке опять рассчитывается тангенс, дает прямую L. В конце концов, через точку xm
,ym
мы проводим прямую L, параллельную L. Точка, в какой ровная L пересечется с ординатой, восстановленной из x=xm+1
=xm
+h, и будет разыскиваемой точкой xm+1
,ym+1
.
Тангенс угла наклона прямой L и прямой L равен
Ф(xm
,ym
,h)=½[f(xm
,ym
)+f(xm
+h,ym
+y¢m
h)] 1.2
где y¢m
=f(xm
,ym
) 1.3
Уравнение полосы L при всем этом записывается в виде
y=ym
+(x-xm
)Ф(xm
,ym
,h),
так что
ym
+1
=ym
+hФ(xm
,ym
,h). 1.4
Соотношения 1.2, 1.3, 1.4 обрисовывают исправленный способ Эйлера.
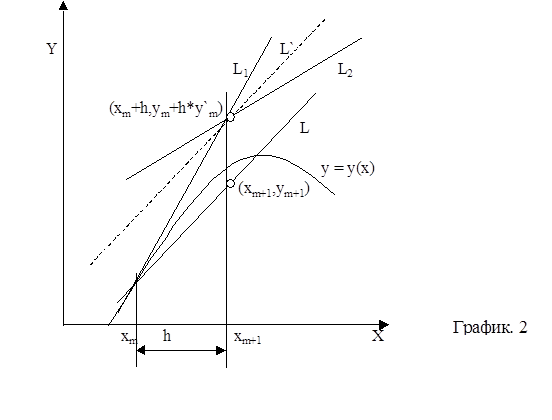
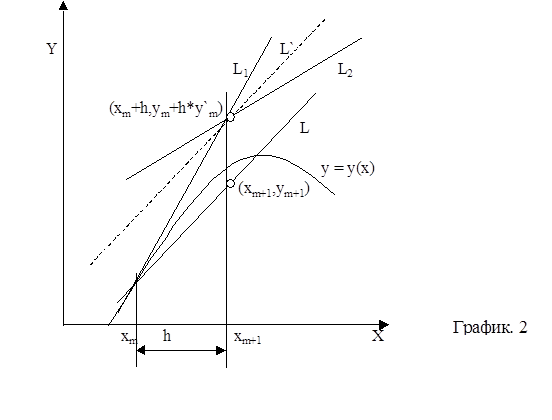
Чтоб узнать, как отлично этот способ согласуется с разложением в ряд Тейлора, вспомним, что разложение в ряд функции f(x,y) можно записать последующим образом:
f(x,y)=f(xm
,ym
)+(x-xm
)¶f/¶x+(y-ym
)¶f/¶x+¼1.5
где личные производные рассчитываются при x=xm
и y=ym
.
Подставляя в формулу 1.5 x=xm
+h и y=ym
+hy¢m
и используя выражение 1.3 для y¢m
, получаем
f(xm
+h,ym
+hy¢m
)=f+hfx
+hffy
+O(h2),
где опять функция f и ее производные рассчитываются в точке xm
,ym
. Подставляя итог в 1.2 и производя нужные преобразования, получаем
Ф(xm
,ym
,h)=f+h/2(fx
+ffy
)+O(h2).
Подставим приобретенное выражение в 1.4 и сравним с Тейлора
ym+1
=ym
+hf+h2/2(fx
+ffy
)+O(h3).
Как лицезреем, исправленный способ Эйлера согласуется с разложением в ряд Тейлора прямо до членов степени h2, являясь, таковым образом, способом Рунге-Кутты второго порядка.
Разглядим модификационный способ Эйлера. Разглядим рис.3 где первоначальное построение изготовлено так же, как и на рис.2. Но сейчас мы берем точку, лежащую на пересечении данной прямой и ординатой x=x+h/2. На рисунке эта точка образована через Р, а ее ордината равна y=ym
+(h/2)y¢m
. Вычислим тангенс угла наклона касательной в данной точке
Ф(xm
,ym
,h)=f+(xm
+h/2,ym
+h/2*y¢m
),1.6
где y¢m
=f(xm
,ym
) 1.7
Ровная с таковым наклоном, проходящая через Р, обозначена через L*. Вослед за тем, мы проводим через точку xm,ym прямую параллельную L*, и обозначаем ее через L0
. Пересечение данной прямой с ординатой x=xm
+h и даст разыскиваемую точку xm+1
,ym+1
. Уравнение прямой можно записать в виде y=ym
+(x-xm
)Ф(xm
,ym
,h),
где Ф задается формулой 1.6. Потому
ym+1
=ym
+hФ(xm
,ym
,h) 1.8
Соотношения 1.6, 1.7, 1.8 обрисовывают так именуемый модификационный способ Эйлера и является еще одним способом Рунге-Кутта второго порядка. Обобщим оба способа. Заметим, что оба способа описываются формулами вида
ym+1
=ym
+hФ(xm
,ym
,h) 1.9
и в обоих вариантах Ф имеет вид
Ф(xm
,ym
,h)=a1
f(xm
,ym
)+a2
f(xm
+b1
h,ym
+b2
hy¢m
),1.10
где y¢m
=f(xm
,ym
) 1.11
А именно, для исправленного способа Эйлера
a1
=a2
=1/2;
b1
=b2
=1.
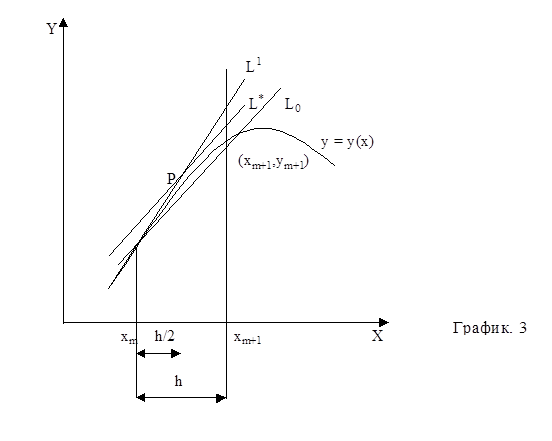
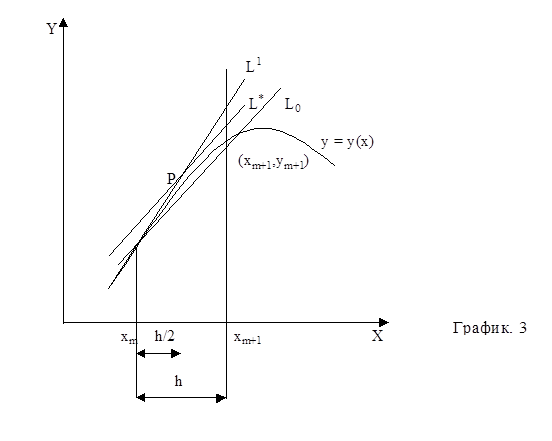
В то время как для модификационного способа Эйлера
a1
=0, a2
=1,
b1
=b2
=1/2.
Формулы 1.9, 1.10, 1.11 обрисовывают некий способ типа Рунге-Кутты. Поглядим, какого порядка способ можно рассчитывать получить в наилучшем случае и каковы допустимые значения характеристик a1
, a2
, b1
и b2
.
Чтоб получить соответствие ряду Тейлора прямо до членов степени h, в общем случае довольно 1-го параметра. Чтоб получить согласование прямо до членов степени h2, будет нужно еще два параметра, потому что нужно учесть члены h2fx
и h2ffy
. Потому что у нас имеется всего четыре параметра, три из которых потребуются для сотворения согласования с Тейлора прямо до членов порядка h2, то самое наилучшее, на что тут можно рассчитывать — это способ второго порядка.
В разложении f(x,y) в ряд 1.5 в округи точки xm
,ym
положим x=xm
+b1
h,
y=ym
+b2
hf.
Тогдаf(xm
+b1
h,ym
+b2
hf)=f+b1
hfx
+b2
hffy
+O(h2),где функция и производные в правой части равенства вычислены в точке xm
,ym
.
Тогда 1.9 можно переписать в виде ym+1=ym+h[a1f+a2f+h(a2b1fx+a2b2ffy)]+O(h3).
Сравнив эту формулу с разложением в ряд Тейлора, можно переписать в виде
ym+1
=ym
+h[a1
f+a2
f+h(a2
b1
fx
+a2
b2
ffy
)]+O(h3).
Если востребовать совпадения членов hf, то a1
+a2
=1.
Сравнивая члены, содержащие h2fx
, получаем a2
b1
=1/2.
Сравнивая члены, содержащие h2ffy
, получаем a2
b2
=1/2.
Потому что мы пришли к трем уравнениям для определения 4 неведомых, то одно из этих неведомых можно задать произвольно, исключая, быть может, нуль, зависимо от того, какой параметр взять в качестве случайного.
Положим, к примеру, a2
=w¹0. тогда a1
=1-w, b1
=b2
=1/2w и соотношения 1.9, 1.10, 1.11 сведутся к
ym+1
=ym
+h[(1-w)f(xm
,ym
)+wf(xm
+h/2w,ym
+h/2wf(xm
,ym
))]+O(h3) 1.12
Это более общая форма записи способа Рунге-Кутта второго порядка. При w=1/2 мы получаем исправленный способ Эйлера, при w=1 получаем модификационный способ Эйлера. Для всех w, хороших от нуля, ошибка ограничения равна
et
=kh31.13
способы Рунге-Кутта третьего и 4-ого порядков можно вывести совсем аналогично тому, как это делалось при выводе способов первого и второго порядков. Мы не будем воспроизводить выкладки, а ограничимся тем, что приведем формулы, описывающие способ 4-ого порядка, один из самых употребляемых способов интегрирования дифференциальных уравнений. Этот традиционный способ Рунге-Кутта описывается системой последующих 5 соотношений
ym+1
=ym
+h/6(R1
+2R2
+2R3
+R4
) 1.14
где R1
=f(xm
,ym
),1.15
R2
=f(xm
+h/2,ym
+hR1
/2),1.16
R3
=f(xm
+h/2,ym
+hR2
/2),1.17
R4
=f(xm
+h/2,ym
+hR3
/2). 1.18
Ошибка ограничения для этого способа равна et
=kh5
так что формулы 1.14-1.18 обрисовывают способ 4-ого порядка. Заметим, что при использовании этого способа функцию нужно вычислять четыре раза.
3. Выбор способа реализации программки
Исходя из вышеизложенного, для решения систем дифференциальных уравнений мы избираем более четкий способ решения – способ Рунге-Кутта 4 порядка, один из самых употребляемых способов интегрирования дифференциальных уравнений.
4. Б
лок-схема программмы










Вход
f1,C[1],C[2],C[3]
f1,k1,k2,k3,k4
f1,Xn,Xk,dp,n,eps,p
выход


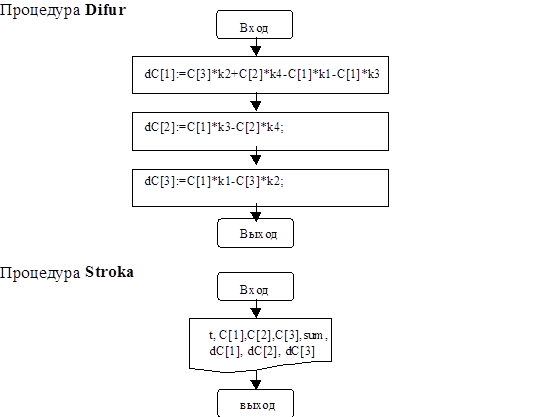
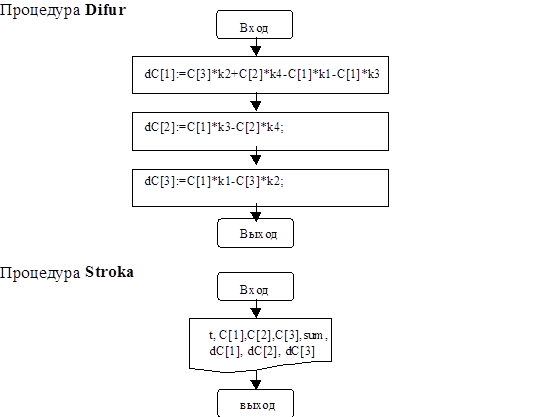
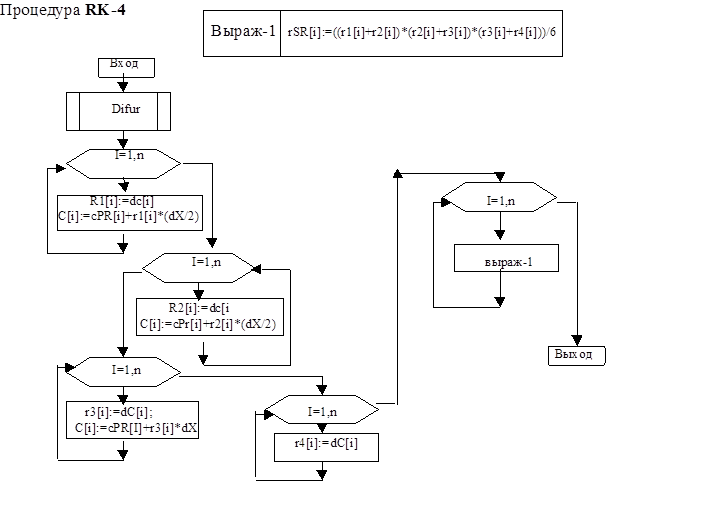
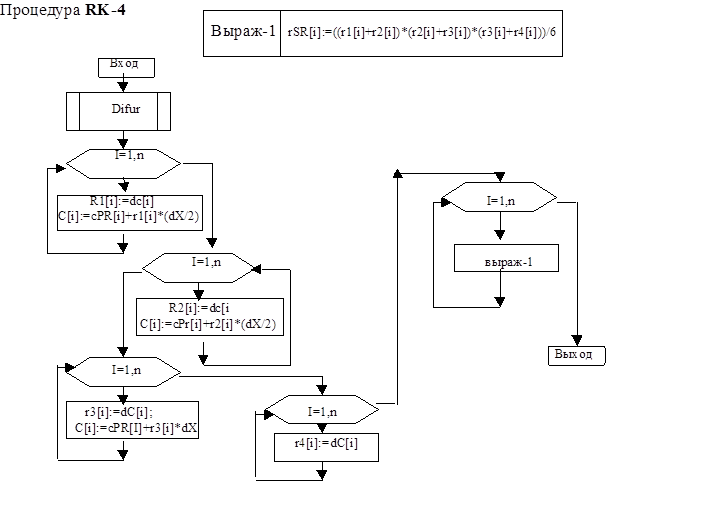
5.
программка
PROGRAM smith_04;USES crt; VAR i,n:integer; sum,k1,k2,k3,k4,p,dp,eps,Xn,Xk,X,dX:real; rSR,C,dC,r1,r2,r3,r4,cPR:array[1..3] of real;
f1,f2:text;
PROCEDURE Difur;
BEGIN
dC[1]:=C[3]*k2+C[2]*k4-C[1]*k1-C[1]*k3; {dcA}
dC[2]:=C[1]*k3-C[2]*k4; {dcB}
dC[3]:=C[1]*k1-C[3]*k2; {dcC}
END;
PROCEDURE RK_4;
BEGIN
Difur;
FOR i:=1 TO n DO BEGIN
r1[i]:=dC[i];
C[i]:=cPR[i]+r1[i]*(dX/2);
END;
Difur;
FOR i:=1 TO n DO BEGIN
r2[i]:=dC[i];
C[i]:=cPr[i]+r2[i]*(dX/2);
END;
Difur;
FOR i:=1 TO n DO BEGIN
r3[i]:=dC[i];
C[i]:=cPR[I]+r3[i]*dX;
END;
Difur;
FOR i:=1 TO n DO r4[i]:=dC[i];
FOR i:=1 TO n DO rSR[i]:=((r1[i]+r2[i])*(r2[i]+r3[i])*(r3[i]+r4[i]))/6;
END;
PROCEDURE STROKA;
BEGIN
WRITE(f2,’|’,x:4:1,’|’,c[1]:7:3,’|’,c[2]:7:3,’|’,c[3]:7:3,’|’);
WRITE(f2,sum:3:0,’|’,dc[1]:7:3,’|’,dc[2]:7:3,’|’,dc[3]:7:3,’|’);
WRITELN(f2);
END;
PROCEDURE RUN;
BEGIN
WRITE(‘Step 3: Calculating data and writting results to file : out.rez’);
X:=Xn;
dX:=0.05;
REPEAT
IF (ABS(x-p)<eps) THEN BEGIN
Difur;
sum:=C[1]+C[2]+C[3];
STROKA;
p:=p+dp; END;
FOR i:=1 TO n DO Cpr[i]:=C[i];
RK_4;
X:=X+dX;
UNTIL(X>Xk);
WRITELN(‘ — done.’);
END;
PROCEDURE INIT;
BEGIN
ClrScr;
WRITELN(‘Smith-04: v1.0 (c) 1998 by Mike Smith smith01@home.bar.ru ‘);
WRITELN;
WRITELN;
WRITE(‘Step 1: Read data from file : in.dat’);
ASSIGN(f1,’in.dat’);
RESET(f1);
READLN(f1,C[1],C[2],C[3]);
READLN(f1,k1,k2,k3,k4);
READLN(f1,Xn,Xk,dp,n,eps,p);
WRITELN(‘ — done.’);
ASSIGN(f2,’out.rez’);
REWRITE(f2);
WRITE(‘Step 2: Write header to file : out.rez’);
WRITELN(f2,»);
WRITELN(f2,’| t,c| Ca,% | Cb,%| Cc,% | SUM | dCa | dCb | dCc |’);
WRITELN(f2,’=’);
WRITELN(‘ — done.’);
END;
PROCEDURE DONE;
BEGIN
WRITELN(‘Step 4: Close all files and exiting…’);
CLOSE(f1);
WRITELN(f2,’=’);
CLOSE(f2);
WRITELN;
END;
BEGIN
INIT;
RUN;
DONE;
END.
6. идентификация переменных
Таблица 1


7. Результаты расчета
Таблица 2
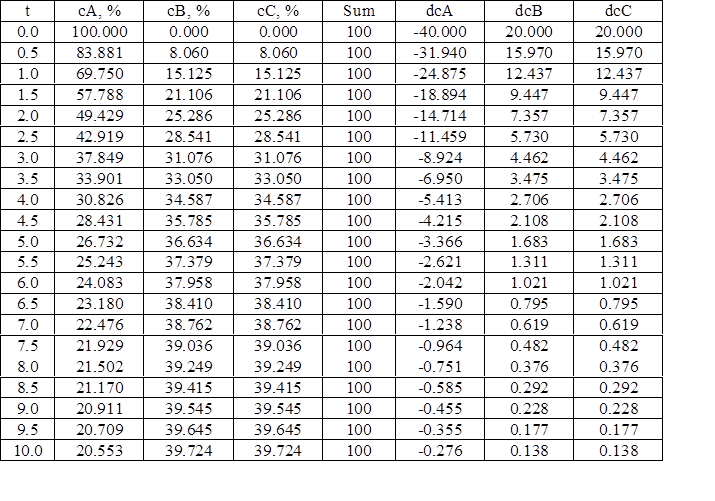

8. Обсуждение результатов расчета.
В итоге расчета кинетической схемы процесса на языке Паскаль способом Рунге-Кутты, были получены результаты зависимости конфигурации концентрации реагирующих веществ во времени. Исходя из приобретенных результатов, можно прийти к выводу, что расчет произведен правильно,
потому что, исходя из приобретенных значений скоростей реакций можно прийти к выводу, что соблюдается баланс скоростей хим реакции.
Разглядим процесс подробнее. Вещество А в протяжении всего процесса расходуется на образование веществ В и С. Концентрации вещества А в исходный момент времени расходуется резвее, чем концентрации его же в конце процесса. Это обосновано тем, что скорость хим реакции зависит от концентрации реагирующего вещества. Производная имеет символ «минус». Это гласит о том, что вещество расходуется. Как следует, чем выше концентрация вещества, вступающего в процесс, тем выше скорость его реагирования с иными субстанциями. Вещества В и С образуются пропорционально, потому что, исходя из кинетической схемы процесса и значений констант скоростей хим реакции, видно, что образование этих веществ и расходование этих веществ,
. Производная имеет символ
. Это гласит о том, что вещество
График. 4
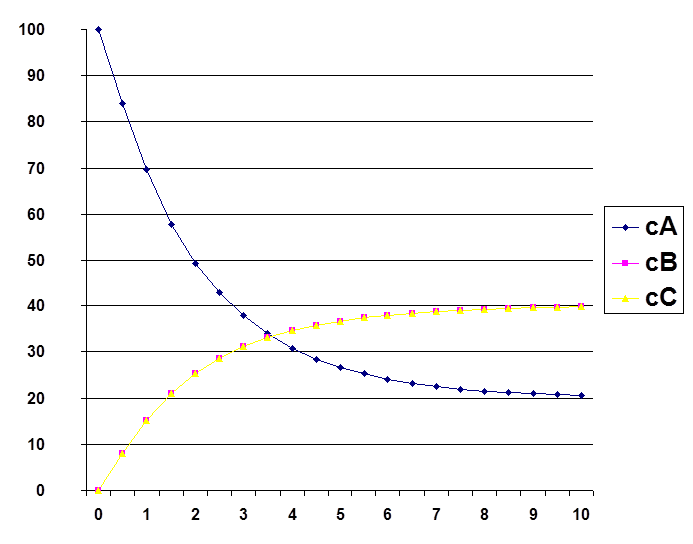

Это видно также и по результатам расчета, в протяжении всего времени исследования процесса концентрации и скорости веществ В и С схожи. В этом можно убедиться по виду графической зависимости концентрации веществ В и С от времени.
Можно сказать, что
В и С и
А. процесс будет протекать до момента установления равновесия, но в данном случае равновесие не установлено, потому что вещества продолжают расходоваться и создаваться. В протяжении всего процесса ни одно из образующихся веществ не поменяло символ производной. Это гласит о том, что
9.
инструкция
к
программм
е
Итак, программка состоит из 3 главных процедур:
Init
— процедура инициалиации, включающую в себя ввод данных;
Run
— процедура вычисления и обработки результатов, содержит в себе вызов 2-ух вспомогательных процедур Difur
, RK-4
, Stroka
, 1-ая из которых отвечает за вычисление, а крайняя — за вывод результатов в файл в табличном виде;
Done
— процедура подготовки к выходу из программки;
и 3-х вспомогательных:
Difur
— процедура вычисления производных (изменение концентрации веществ за единикцу времени )
RK-4
— используя значения производных, вычисленных процедурой Difur, вычисляет последущие концентрации веществ способом Рунге-Кутта
Stroka
— процедура вывода результата в файл в табличном виде
Разглядим все эти процедуры поподробнее:
Процедура INIT:


В данной процедуре задействованы операторы ввода/вывода Wite/Read
, оператор модуля Crt — CrlScr
— чистка экрана, файлового ввода/вывода — Reset/Rewrite
– открытие файла для чтения и создание новейшего файла, соответственно. Данная процедура делает функцию инициализации программных данных, считывание данных из файла in.dat
, создание, открытие на запись файла out.rez
и запись в него шапки таблицы результатов.
Процедура RUN:
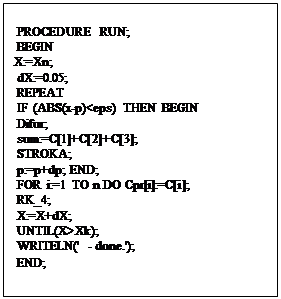

В данной процедуре задействованы операторы цикла Repeat/Until
, и For/Do
c операторами условного перехода IF/Then
. Зависимо от критерий вызываются процедуры Difur и Strok. В теле цикла повсевременно вызывается процедура RK-4вызывающая 4 раза функцию Difur
.
Процедура DONE:


В данной процедуре задействованы оператор работы с файлами Close, который закрывает файлы с начальными данными и файл с приобретенными в резуультате вычислений плодами.
Процедура DIFUR:


Данная процедура вычисляет производную конфигурации концентрации везества за единицу времени.
Процедура STROKA:


Данная процедура при помощи оператора вывода WRITE
записывает результаты в файл, соответственный файловой переменной F2, назначенной коммандой ASSIGN
в процедуре INIT


Процедура RK-4:
Данная процедура, используя вызовы процедур Difur
, также циклы операторы цикла FOR
, вычисляет последуущие концентрации веществ по предидущим точкам.
программка представляет собой 2 файла – файл с начальным текстом на языке Паскаль smith.pas
и исполняемый модуль smith.exe
скомпилированный компилятором TNT Pascal 3.25 компании Layer`s Ins.
Исполняемый модуль программки предназначен для пуска в операционных системах: MS Dos, Windows95, Windows NT, OS/2, также в X-windows под Linux (при наличии эмулятора )
Для обычной работы программке нужно 640 кb «нижней» памяти и 20 kb дискового места. Согласитесь – требования малые, беря во внимание то, что сама программка полностью не требовательна к микропроцессору.
В процессе работы программка считывает данные из файла in.dat
и записывает результаты работы в файл out.rez
в табличном виде. Начальный файл программма открывает обычными средствами ОС, не проверяя его наличие перед работой, потому, если данный файл не будет доступен в каталоге, в каком размещена программка, компилятор выдаст сообщение о ошибке. Если Вы опосля пуска программки узрели что-то типа «Runtime error 202 at 0000:0A86» — это всего только означает, что программка не смогла отыскать файл с начальными данными в текущем каталоге. Если Вы запамятовали поместить его туда,
этот файл в каталог с программкой и
исполняемый модуль снова. Если данный файл у Вас
, Для вас прийдется создать его самому.
Для этого в любом редакторе текста наберите 3 выделенных строки и сохраните сделанный файл с именованием in.dat
100 0 0
0.2 0.1 0.2 0.1
0 10 0.5 3 0.05 0
В процессе работы программка будет выдавать сообщения о успешном окончании всякого блока. Если все прошло нормально, то на дисплее собственного компа Вы увидите следуще сообщения:


Step 1: Read data from file : in.dat — done
.
Step 2: Write header to file : out.rez — done
.
Step 3: Calculating data and writting results to file : out.rez — done
.
Step 4: Close all files and exiting…
1-ый шаг (step1) докладывает, что данные из файла in.dat
были удачно прочитаны
2-ой – о том что программка удачно сделала выходной файл out.rez
и записала в него шапку таблицы с данными
В 3-ем сообщении сказано, что данные удачно посчитаны и записаны в выходной файл out.rez
4-ое сообщение докладывает о окончании вычислений и окончании программки.
Опосля того, как программка отработает, Вы можете познакомится с плодами, которые были вычислены и помещены в файл результатов out.rez.
Просмотрев его хоть какой программкой просмотра текстовых файлов либо вывев его на печать, вы получите таблицу c плодами.
10. З
аключение.
В итоге выполнения расчета получена зависимость конфигурации концентрации вещества во времени. Из расчета следует, что в протяжении всего процесса вещество А расходовалось на образование В и С. процесс не достигнул конечного состояния (не достигнул равновесия) Максимум концентрации вещества наблюдался при последующих значениях времени:
при
времени max соответствовал веществу А;
при
, max соответствовал субстанциям B и С,
но, это не является максимумом концентрации веществ в процессе
совершенно, потому что вещества B и С продолжают создаваться;
В процессе выполнения работы был произведен расчет системы дифференциальных уравнений способом Рунге-Кутты 4-ого порядка, произведен расчет кинетической схемы процесса при изотермических критериях при данных значениях концентраций и констант скоростей. Расчет произведен с малой величиной погрешности.
Перечень литературы
1. Мудров А.Е.Численные способы для ПЭВМ на языках Паскаль, Фортран и Бейсик. МП “Раско”, Томск, 1991 г.
]]>
