Учебная работа. Курсовая работа: Поверхности второго порядка
Поверхность второго порядка — геометрическое пространство точек, декартовы прямоугольные координаты которых удовлетворяют уравнению вида
a11
х2
+ а22
у2
+ a33
z2
+ 2a12
xy + 2a23
уz + 2a13
xz + 2а14
x + 2а24
у+2а34
z +а44
= 0 (1)
в каком по последней мере один из коэффициентов a11
, а22
, a33
, a12
, a23 ,
a13
отличен от нуля.
Уравнение (1) мы будем именовать общим уравнением поверхности второго порядка.
Разумеется, поверхность второго порядка, рассматриваемая как геометрический объект, не изменяется, если от данной декартовой прямоугольной системы координат перейти к иной декартовой системе координат. Отметим, что начальное уравнение (1) и уравнение, приобретенное опосля преобразования координат, алгебраически эквивалентны.
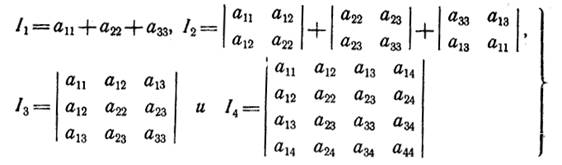
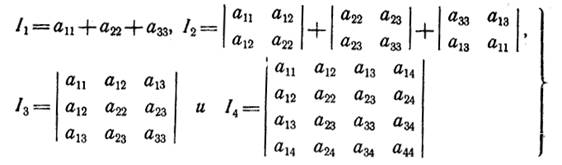
1. Инварианты уравнения поверхности второго порядка.
Справедливо последующее утверждение.
являются инвариантами уравнения (1) поверхности второго-порядка относительно преобразований декартовой системы координат.
Подтверждение этого утверждения приведено в выпуске «Линейная алгебра» реального курса.
§ 2. систематизация поверхностей второго порядка
1. Систематизация центральных поверхностей. Пусть S — центральная поверхность второго порядка. Перенесем начало координат в центр данной для нас поверхности, а потом произведем обычное упрощение уравнения данной для нас поверхности. В итоге обозначенных операций уравнение поверхности воспримет вид
a11
х2
+ а22
у2
+ a33
z2
+ а44
= 0 (2)
Потому что инвариант I3
для центральной поверхности отличен от ноля и его значение, вычисленное для уравнения (2) , равно a11
• а22
• a33
, то коэффициенты a11
,а22
, a33
удовлетворяют условию :
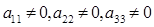
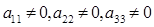
Вероятны последующие случаи :
1. Коэффициенты a11
,а22
, a33
1-го знака, а коэффициент а44
отличен от нуля. В этом случае поверхность S именуется эллипсоидом.
Если коэффициенты a11
,а22
, a33
, а44
1-го знака, то левая часть (2) ни при каких значениях х, у, z не обращается в нуль, т. е. уравнению поверхности S не удовлетворяют координаты никакой точки. В этом случае поверхность S именуется надуманным эллипсоидом.
Если символ коэффициентов a11
,а22
, a33
противоположен знаку коэффициента а44
, то поверхность S именуется вещественным эллипсоидом. В предстоящем термином «эллипсоид» мы будем именовать только вещественный эллипсоид.
Обычно уравнение эллипсоида записывают в канонической форме. Разумеется, числа
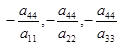
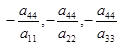
положительны. Обозначим эти числа соответственно а2
, b2
, с2
. Опосля легких преобразований уравнение эллипсоида (2) можно записать в последующей форме:
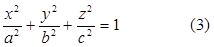
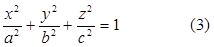
Уравнение (3) именуется каноническим уравнением эллипсоида.
Если эллипсоид задан своим каноническим уравнением (3), то оси Ох, Оу и Оz. именуются его главными осями.
2. Из 4 коэффициентов a11
,а22
, a33
, а44
два 1-го знака, а два остальных—обратного. В этом случае поверхность S именуется однополостным гиперболоидом.
Обычно уравнение однополостного гиперболоида записывают в канонической форме. Пусть, ради определенности, a11
> 0, а22
> 0, a33
< 0, а44
< 0. Тогда числа
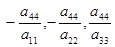
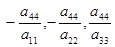
положительны. Обозначим эти числа соответственно а2
, b2
, с2
. Опосля легких преобразований уравнение (2) однополостного гиперболоида можно записать в последующей форме:
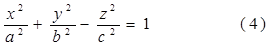
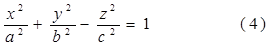
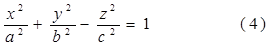
Уравнение (4) именуется каноническим уравнением однополостного гиперболоида.
Если однополостный гиперболоид задан своим каноническим уравнением (4), то оси Ох, Оу и Oz именуются его главными осями.
3. символ 1-го из первых 3-х коэффициентов a11
,а22
, a33
, а44
противоположен знаку других коэффициентов. В этом случае поверхность S именуется двуполостным гиперболоидом.
Запишем уравнение двуполостного гиперболоида в канонической форме. Пусть, ради определенности, a11
< 0, а22
< 0, a33
> 0, а44
< 0. Тогда :
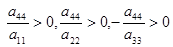
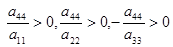
Обозначим эти числа соответственно через a2
, b2
, с2
. Поcли легких преобразований уравнение (2) двуполостного гиперболоида можно записать в последующей форме:
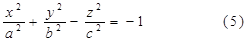
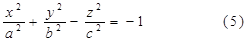
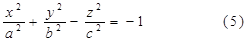
Уравнение (5) именуется каноническим уравнением двуполостного гиперболоида.
Если двуполостный гиперболоид задан своим каноническим уравнением, то оси Ох, Оу и Оz именуются его главными осями.
4. Коэффициент а44
равен нулю. В этом случае поверхность S именуется конусом второго порядка.
Если коэффициенты a11
, а22
, a33
1-го знака, то левая часть (2) обращается в нуль (а44
= 0) только для х=у=z=0, т. е. уравнению поверхности S удовлетворяют координаты лишь едной точки. В этом случае поверхность S именуется надуманным конусом второго порядка. Если коэффициенты a11
, а22
, a33
имеют различные знаки, то поверхность S является вещественным конусом второго порядка.
Обычно уравнение вещественного конуса второго порядка записывают в канонической форме. Пусть, ради определенности,
a11
> o, а22
> 0, a33
< 0. Обозначим
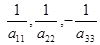
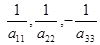
соответственно через а2
, b2
, с2
. Тогда уравнение (2) можно записать в виде
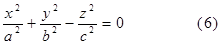
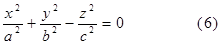
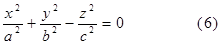
Уравнение (6) именуется каноническим уравнением вещественного конуса второго порядка.
2. Систематизация нецентральных поверхностей второго порядка.
Пусть S — нецентральная поверхность второго порядка, т. е. поверхность, для которой инвариант I3
равен нулю. Произведем обычное упрощение уравнения данной для нас поверхности. В итоге уравнение поверхности воспримет вид
a´11
х´2
+ а´22
у´2
+ a´33
z´2
+ 2а´14
x´ + 2а´24
у´+2а´34
z´ +а´44
= 0 (7)
для системы координат Ox´y´z´
Потому что инвариант I3
= 0 и его
a´11
• а´22
• a´33
, то один либо два из коэффициентов a´11
, а´22
, a´33
равны нулю. В согласовании с сиим разглядим последующие вероятные случаи.
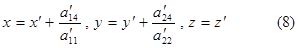
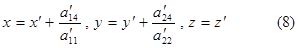
1. один из коэффициентов a´11
, а´22
, a´33
равен нулю. Ради определенности будем считать, что a´33
= 0 (если равен нулю какой-нибудь иной из обозначенных коэффициентов, то можно перейти к рассматриваемому случаю методом переименования осей координат). Перейдем от координат х’, у’, z’ к новеньким координатам х, у, z по формулам
Подставляя х’, у’ и z’, отысканные из (8), в левую часть (7) и заменяя потом
a´11
на a11
, а´22
на а22
, а´34
на pи а´44
на q, получим последующее уравнение поверхности S в новейшей системе координат Oxyz :
a11
х2
+ а22
у2
+ 2pz + q = 0 (9)
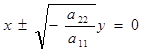
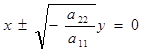
1) Пусть р = 0, q = 0. поверхность S распадается на пару плоскостей
При всем этом, разумеется, эти плоскости будут надуманными, если знаки a11
и а22
схожи, и вещественными, если знаки a11
и а22
различны.
2) Пусть р = 0, q ≠ 0. Уравнение (9) воспринимает вид
a11
х2
+ а22
у2
+ q = 0 (10)
Понятно, что уравнение (10) является уравнением цилиндра с образующими, параллельными оси Оz. При всем этом если a11
, а22
, q имеют однообразный символ, то левая часть (10) отлична от нуля для всех х и y, т. е. цилиндр будет надуманным. Если же посреди коэффициентов a11
, а22
, q имеются коэффициенты различных символов, то цилиндр будет вещественным. Отметим, что в случае, когда a11
и а22
имеют схожие знаки, aq — обратный, то величины положительны.
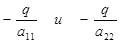
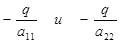
Обозначая их соответственно через а2
и b2
, мы приведем уравнение (10) к виду
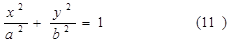
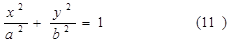
Таковым образом, в отмеченном случае мы имеем эллиптический цилиндр. В случае, a11
и а22
имеют разные знаки, мы получим гиперболический цилиндр. Просто убедиться, что уравнение гиперболического цилиндра быть может приведено к виду
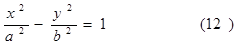
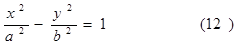
3) Пусть р≠0. Произведем параллельный перенос системы координат, выбирая новое начало в точке с координатами
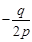
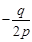
(0, 0, ).
При всем этом оставим старенькые обозначения координат х, у, z. Разумеется, для того чтоб получить уравнение поверхности S в новейшей системе координат, довольно поменять в уравнении (9)
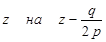
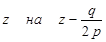
Получим последующее уравнение:
a11
х2
+ а22
у2
+ 2pz= 0 (13)
Уравнение (13) описывает так именуемые параболоиды. При этом если a11
и а22
имеют однообразный символ, то параболоид именуется эллиптическим. Обычно уравнение эллиптического параболоида записывают в канонической форме:
Уравнение (14) просто выходит из (13). Если a11
и а22
имеют различные знаки, то параболоид именуется гиперболическим. Каноническое уравнение гиперболического параболоида имеет вид
Это уравнение также просто быть может получено из (13).
— 2°. Два из коэффициентов a´11
, а´22
, a´33
равны нулю. Ради определенности будем считать, что a´11
= 0 и а´22
= 0 Перейдем от х,’, у’, z’ к. новеньким координатам х, у, z по формулам :
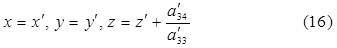
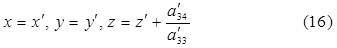
Подставляя х’, у’ и z’ , отысканные из (16) в левую часть (7) и заменяя потом a´33
на a33 ,
a´14
на р , a´24
на q и a´44
на r , получим последующее уравнение поверхности S в новейшей системе координат Охуz :
a33
z2
+ 2px + 2qy + r = 0 (17)
1) Пустьр=0, q=0. поверхность S распадается на пару параллельных плоскостей
При всем этом, разумеется, эти плоскости будут надуманными, если знаки a33
и r схожи, и вещественными, если знаки a33
и r различны, при этом при r = 0 эти плоскости соединяются в одну.
2) Хотя бы один из коэффициентов р либо q отличен от нуля. В этом случае повернем систему координат вокруг оси Oz так, чтоб новенькая ось абсцисс стала параллельной плоскости 2рх+2qy+r=0. Просто убедиться, что при таком выборе системы координат, при условии сохранения обозначения х, у и z для новейших координат точек, уравнение (17) воспримет вид
a33
z2
+ 2q´y= 0 (19)
которое является уравнением параболического цилиндра с образующими, параллельными новейшей оси Ох.
§ 3. исследование формы поверхностей второго порядка по их каноническим уравнениям
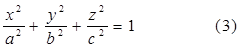
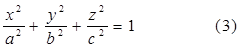
1. Эллипсоид.
Из уравнения (3) вытекает, что координатные плоскости являются плоскостями симметрии эллипсоида, а начало координат—центром симметрии. Числа а, b, с именуются полуосями эллипсоида и представляют собой длины отрезков, от начала координат до точек пересечения эллипсоида с осями координат. Чтоб наиболее наглядно представить для себя форму эллипсоида, выясним форму линий пересечения его плоскостями, параллельными какой-нибудь из координатных плоскостей.
Ради определенности разглядим полосы Lh
пересечения эллипсоида с плоскостями
z= h (20)
параллельными плоскости Оху. Уравнение проекции L*
h
полосы Lh
на плоскость Оху выходит из уравнения (3), если положить в нем z= h. Таковым образом, уравнение данной для нас проекции имеет вид
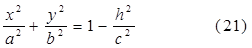
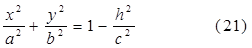
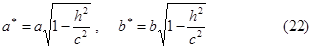
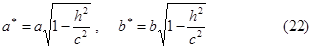
Если положить
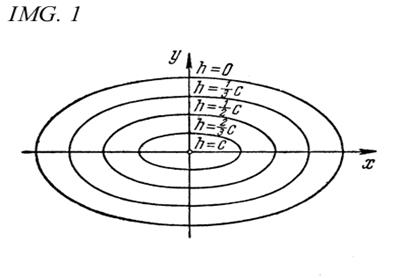
то уравнение (21) можно записать в виде
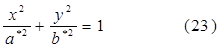
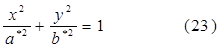
т. е. L*
h
представляет собой эллипс с полуосями а* и b*, которые могут быть вычислены по формулам (22). Потому что Lh
выходит «подъемом» L*
h
на высоту h по оси Оz(см. (20)), то и Lh
представляет собой эллипс.
должен быть «поднят» этот эллипс. Мы получим собственного рода «карту» эллипсоида. Используя эту «карту», просто представить для себя пространственный вид эллипсоида.
(способ представления формы фигуры методом получения «карты» фигуры я привожу лишь для эллипсоида, представить форму остальных фигур сиим способом можно аналогично)
Приятное изображение эллипсоида находится на последующей страничке.
Эллипсоид
.
2. Гиперболоиды.
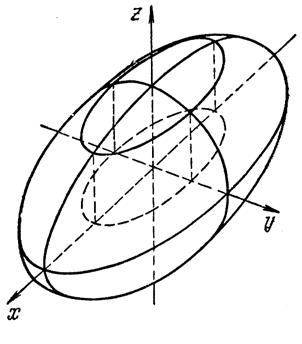
1. Однополостный гиперболоид. Обратимся к каноническому уравнению (4) однополостного гиперболоида
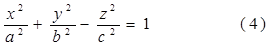
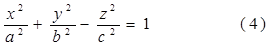
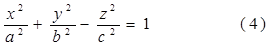
Из уравнения (4) вытекает, что координатные плоскости являются плоскостями симметрии, а начало координат — центром симметрии однополостного гиперболоида.
2. Двуполостный гиперболоид.
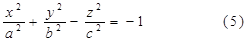
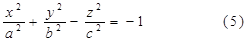
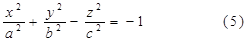
Из канонического уравнения (5) двуполостного гиперболоида вытекает, что координатные плоскости являются его плоскостями симметрии, а начало координат — его центром симметрии.
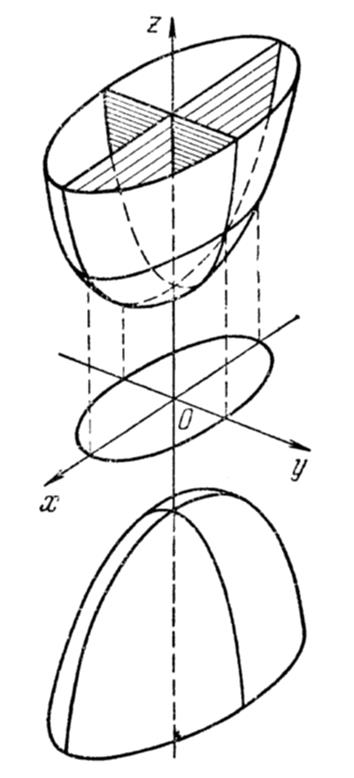
3. Параболоиды.
1. Эллиптический параболоид. Обращаясь к каноническому уравнению (14) эллиптического параболоида
мы лицезреем, что для него Oxz и Оуz являются плоскостями симметрии. Ось Oz, представляющая линию пересечения этих плоскостей, именуется осью эллиптического параболоида.
2. Гиперболический параболоид. Из канонического уравнения (15) гиперболического параболоида вытекает, что плоскости Oxz и Оуz являются плоскостями симметрии. Ось Oz именуется осью гиперболического пaраболоида.
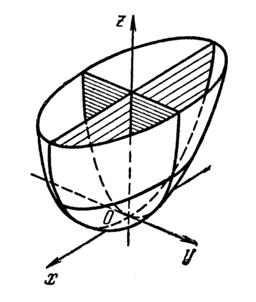
Прим.: получение «карты высот» для гиперболического пaраболоида несколько различается от аналогичной процедуры для вышеприведенных поверхностей 2-го порядка, потому я также включил его в собственный реферат.
Полосы z=h пересечения гиперболического параболоида плоскостями z=h представляют собой при h>0 гиперболы
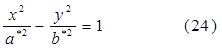
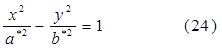
с полуосями
а при h < 0 —сопряженные гиперболы для гипербол (24)
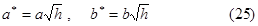
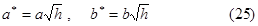
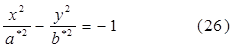
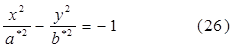
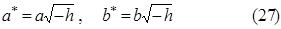
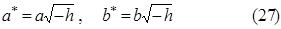
с полуосями
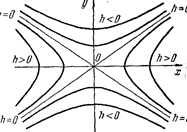
Используя формулы (24)—(27), просто выстроить «карту» гиперболического параболоида. Отметим еще, плоскость z=0 пересекает гиперболический параболоид по двум прямым :
Из формул (25) и (27) вытекает, что прямые (28) являются асимптотами гипербол (24) и (26).
карта гиперболического параболоида дает представление о его пространственной форме. Как и в случае эллиптического параболоида, можно убедиться в том, что гиперболический параболоид быть может получен методом параллельного перемещения параболы, представляющей собой сечение плоскостью Oxz (Оуz), когда ее верхушка движется вдоль параболы, являющейся сечением параболоида плоскостью Oyz (Oxz).
Прим.: Изображение гиперболического пaраболоида дано на последующей страничке.
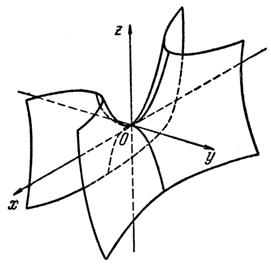
Гиперболический параболоид.
4. Конус и цилиндры второго порядка.
— 1°. Конус второго порядка
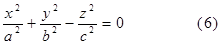
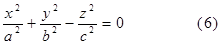
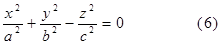
Убедимся, что вещественный конус S образован прямыми линиями, проходящими через начало О координат. естественно именовать точку О верхушкой конуса.
Для подтверждения сформулированного утверждения, разумеется, довольно установить, что ровная L, соединяющая произвольную, лучшую от начала координат точку
М0
(х0
, у0
, z0
) конуса (6) и начало координат О , полностью размещается на конусе, т. е. координаты (х, у, z) хоть какой точки М прямой L удовлетворяют уравнению (6).
Потому что точка М0
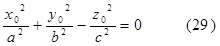
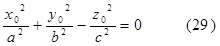
(х0
, у0
, z0
) лежит на конусе (6), то :
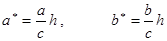
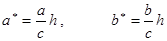
Координаты (х, у, z) хоть какой точки М прямой L равны соответственно tx0
, ty0
, tz0
, где t—некое число. Подставляя эти значения для х, у и z в левую часть (6), вынося потом t2
за скобку и беря во внимание (29), мы убедимся в том, что М лежит на конусе. Таковым образом, утверждение подтверждено.
Состоит из прямых линий, параллельных оси Oz.
3. Гиперболический цилиндр.
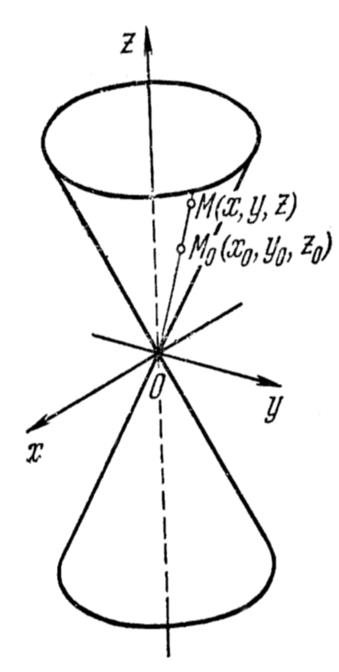
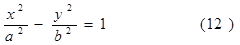
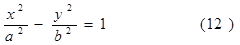
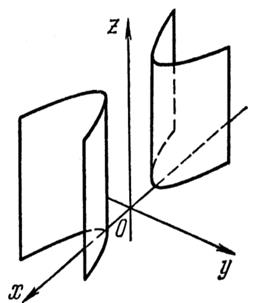
Состоит из прямых линий, параллельных оси Oz.
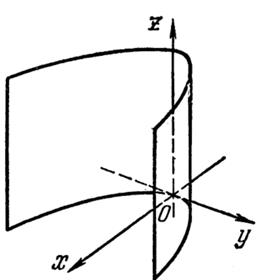
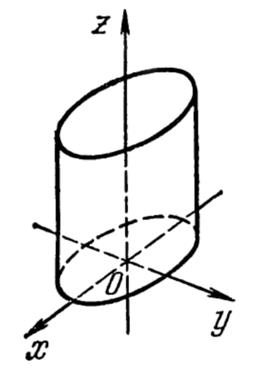
4. Параболический цилиндр.
a33
z2
+ 2q´y= 0 (19)
Методом переименования осей координат и обычных арифметических операций из уравнения, (19) мы получим новое, малогабаритное уравнение параболического цилиндра.
Перечень литературы.
В.А. Ильин, Э.Г. Позняк «Аналитическая геометрия»
]]>