Учебная работа. Реферат: Скалярная проекция гиперкомплексных чисел
Введение.
При первой же попытке рассмотрения гиперкомплексных чисел в качестве основания для соответственной геометрии возникает желание отыскать в гиперкомплексных числах аналоги геометрических понятий. И одной из первых проблем становится поиск аналога скалярного произведения. Если в геометрии есть понятие соответствует в гиперкомплексных числах?
Рвение к общности определения наталкивается на ряд понятий, которые оказались введены в традиционном подходе в виде, как молвят студенты, “подгонки”. И скалярное произведение, и сопряжение, как оказывается, были введены в арифметику аксиоматически и аксиомы, использоваашие их определение, естественным образом подтвердили их характеристики, вытекающие конкретным образом из их определения.
Традиционная форма (билинейная форма) была применена, к примеру, в аксиоме Гурвица и тем было введено ограничение на набор рассматриваемых алгебр. Последующие пробы развития теории гиперкомплексных алгебр пошли не по пути рассмотрения параметров алгебр, образующихся методом удвоения и использования этих параметров, а по пути рассмотрения алгебр над полями со все наиболее глубочайшей их структуризацией.
Мне хотелось бы до конца узнать вопросец — что является аналогом скалярного произведения в гиперкомплексных числах и, сравнив два подхода, узнать, где находятся белоснежные пятна традиционного подхода. И робко представить направление исследовательских работ, которое может отдать, может быть, полезные в технике и физике результаты.
Скалярное же произведение в традиционной геометрии, определяемое в виде билинейной формы, к гиперкомплексным числам не подступает в общем случае, так как автоматом значит и требование билинейности квадрата модуля. А таковым требованиям отвечает наименьшая часть алгебр. Другие имеют определение 4-й степени модуля в виде 4-х линейной формы, либо, может быть, еще наиболее высочайшего порядка.
В данной статье и предпринимается попытка отыскания формально общего определения скалярного произведения в форме, допускающей его применение к таковым алгебрам с 4-х линейными формами.
1. Традиционный подход.
Возьмем на плоскости два вектора
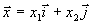
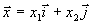
Обозначим концы данных векторов соответственно через X и Y. Из формулы для расстояния меж 2-мя точками имеем:
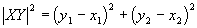
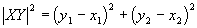
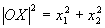
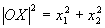
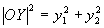
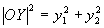
откуда следует
(1)
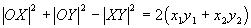
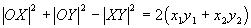
Из этого равенства, если учитывать аксиому Пифагора, просто узреть, что нужным и достаточным условием перпендикулярности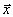 
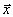
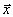
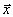
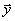
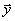
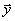
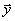
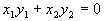
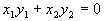
и 
является
Заметим, что если это рассуждение применить к векторам не на плоскости, а в пространстве, то получим условие перпендикулярности в аналогичной форме:
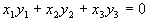
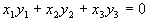
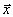
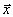
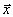
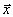
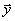
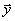
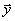
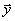
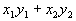
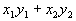
Формула (1) наводит на идея связать с каждой парой векторов и на плоскости число
(2)
а в пространстве — число
(2’)
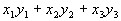
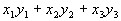
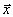
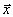
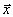
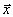
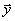
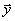
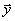
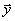
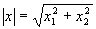
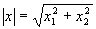
Это число в геометрии именуют скалярным произведением векторов и и обозначают (x,y). Заметим, что длина случайного вектора x выражается через скалярное произведение. А конкретно, в случае плоскости
а в случае места
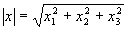
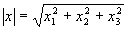
Вышеприведенный ход рассуждений взят из книжки [1] и является собственного рода прототипом. Отмечу снова, что скалярное произведение вводится на базе аксиомы Пифагора, а не напротив, как время от времени пробуют обосновать ленивые студенты.
К главным свойствам скалярного произведения относят:
1) 
, при этом (x,x) лишь при x = 0
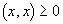
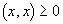
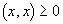
2) (x,y) = (y,x)
3) (x,ky) = k(x,y) где k — хоть какое действительное число
4) (x,y+z)=(x,y)+(x,z)
При любом обобщении, как пишут Кантор и Солодовников, понятия скалярного произведения на n — мерный вариант лучше, чтоб характеристики 1) — 4) сохранили силу. Ввиду этого примем последующее определение.
Определение. Будем гласить, что в n — мерном векторном пространстве An
задано скалярное произведение, если каждым двум векторам x и y сопоставлено некое действительное число — обозначим его (x,y) — так, что выполнены характеристики 1), 2), 3), 4). Число (x,y) будем именовать скалярным произведением вектора x на вектор y.
В наиболее общем виде скалярное произведение определяется как
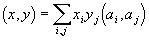
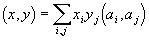
где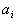 
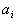
— базовые вектора.
Величины
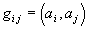
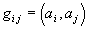
являются неизменными числами, зависящими лишь от избранного базиса. Таковым образом, если избран базис, то
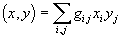
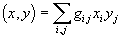
Вышеприведенное традиционное определение скалярного произведения сыграло в арифметике собственного рода роль фундамента, при этом очень крепкого и основательного. И к большенному огорчению таковой подход не отдал результатов в финслеровых геометриях, когда величина вектора определяется не через билинейную форму, а через n — линейную.
2. Геометрическая трактовка проекции.
Для введения определения скалярного произведения в форме, допустимой к использованию, разглядим принцип формирования проекции и попробуем ее формализовать. Обратим внимание на обыденные вектора в 2-х либо 3-х мерном пространстве.
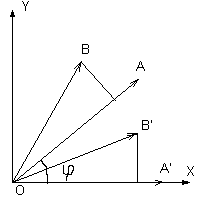
Проекцией назовем величину, равную расстоянию от начала координат до точки пересечения вектора A с перпендикуляром, построенным на него из точки B. сейчас представим для себя, что место — это место компонент гиперкомплексного числа, и означает выстроить перпендикуляр мы пока не можем, так как это понятие еще не определено.
Сейчас повернем оба наших аектора так, чтоб вектор A совпал с одной из осей. В этом случае проекция вектора B на вектор A определяется в особенности просто — нужно взять компоненту, подобающую оси X, и эта величина и будет проекцией.
Для того, чтоб этот способа работал в произвольно взятой системе гиперкомплексных чисел Кэли — Диксона, выберем в качестве таковой мотивированной оси для доворота действительную ось, так как в хоть какой алгебре Кэли — Диксона определена действительная компонента.
Отметим тот факт, что поворот должен осуществляться в плоскости, проходящей через действительную ось и мы можем применять механизм скалярно — пространственных поворотов, описанный в работе [2]. В случае использования алгебр, коммутативных по умножению, поворот быть может осуществлен так же, как на обыкновенной всеохватывающей плоскости, методом обычного умножения на оператор поворота.
3. Скалярная
Будучи примененным к вектору A, этот поворот должен отдать действительное число:
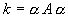
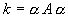
Нетрудно созидать, что этому уравнению удовлетворяет решение
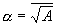
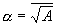
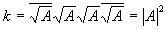
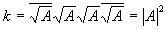
Либо, по другому говоря, сам вектор A и задает оператор поворота, на который следует его повернуть, чтоб получить действительное число.
Применив этот оператор поворота к вектору B, получим:
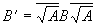
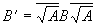
И для того, чтоб получить проекцию, следует взять действительную часть вектора B’ и провести подобающую нормировку, так как обозначенным поворотом мы исказили величину модуля вектора B.
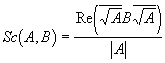
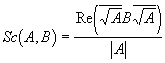
К числу очень принципиальных параметров скалярного произведения относится:
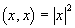
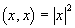
Потому, стремясь отыскать для гиперкомплексных чисел полную аналогию скалярному произведению, мы не будем применять нормировок. В этом случае определенное выше правило смотрится как:
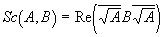
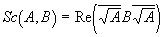
И для варианта A = B перебегает в
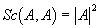
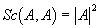
Перечислим снова характеристики скалярного произведения в традиционном варианте и найдем соответствия им в случае гиперкомплексных чисел:
1) , при этом (x,x) лишь при x = 0
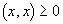
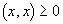
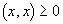
2) (x,y) = (y,x)
3) (x,ky) = k(x,y) где k — хоть какое действительное число
4) (x,y+z)=(x,y)+(x,z)
Для первого характеристики вышеприведенное правило построения проекции не подступает, так как
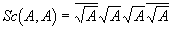
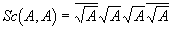
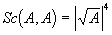
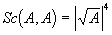
Так как даже для тех алгебр, для которых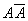 
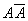
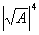
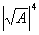
быть может отрицательным числом, число 
постоянно положительно, но исключение составляет условие
(x,x) = 0 лишь при x = 0
здесь следует создать обмолвку, что в гиперкомплексных алгебрах вариант эталонов совсем не является исключением, потому для скалярной проекции гиперкомплексных чисел полностью может быть снять это условие и разрешить
при 
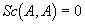
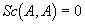
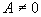
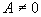
Разглядим 2-ое свойство скалярного произведения
(x,y) = (y,x)
В случае построения аналогии в нашем случае следует обосновать, что
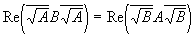
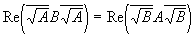
Для этого докажем промежные равенства:
a)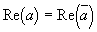 
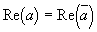
b)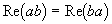 
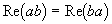
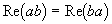
Для подтверждения равенства a) разглядим коэффициенты таблицы произведения надуманных единиц в алгебрах Кэли — Диксона:
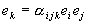
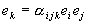
где через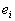 
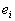
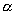
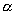
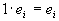
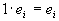
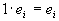
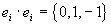
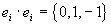
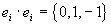
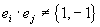
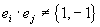
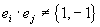
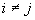
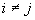
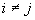
обозначены надуманные единицы гиперкомплексной алгебры, 
— коэффициенты произведений. Для всех гиперкомплексных алгебр Кэли — Диксона, определенных схожей таблицей произведений, производится
при 
Таковым образом, в произведении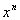 
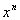
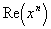
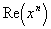
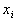
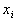
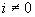
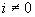
в реальной части 
будут находиться лишь четные степени 
при 
, а нечетных не будет.
Обозначив через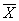 
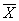
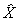
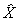
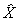
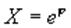
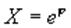
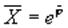
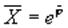
элемент алгебры, алгебраически сопряженный элементу X, а через 
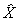
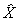
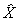
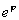
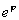
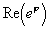
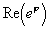
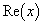
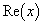
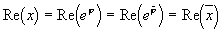
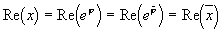
— сопряжение методом смены символов у всех коэффициентов при надуманных единицах, получим:
Сопряжение еще можно именовать фазовым сопряжением, так как сопрягается фаза числа. Так как выражение для 
определено в виде полиномиального ряда, то в 
будут заходить лишь четные функции от надуманных компонент фазы числа X. Так как функции четные, к примеру ch либо cos, то действительная часть 
при алгебраическом сопряжении не изменяется:
Для подтверждения промежного равенства b) разглядим также таблицу произведений надуманных единиц алгебр Кэли — Диксона:
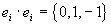
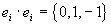
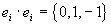
Так как раскрыв произведение ab мы получим гиперкомплексное число, разглядим образование его реальной части. В нее входят:
— произведение реальных частей a и b.
— произведение схожих надуманных компонент a и b.
Так как для алгебр Кэли — Диксона недозволено получить реального числа из произведений
при
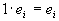
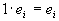
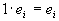
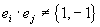
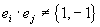
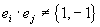
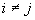
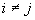
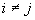
а две вышеприведенные составляющие не зависят от порядка сомножителей a и b, то, как следует,
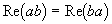
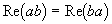
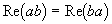
Для подтверждения соответствия предложенной формы скалярной проекции второму свойству скалярного произведения просто преобразуем выражение:
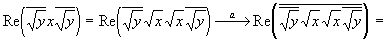
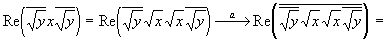
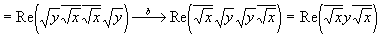
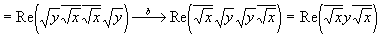
Таковым образом, если скалярному произведению (x,y) сопоставлять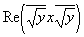 
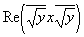
, то правило коммутативности скалярного произведения производится.
Соответствие предлагаемой формы скалярной проекции третьему свойству скалярного произведения проверяется конкретно: если k — действительное число, то
, потому
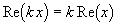
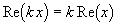
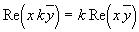
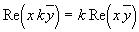
Для проверки соответствия четвертому свойству используем 2-ое и проверим:
(x,y + z) = (y + z,x) = (y,x) + (z,x)
Распишем скалярную проекцию:
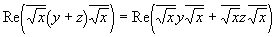
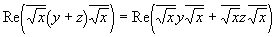
Так как для алгебр Кэли — Диксона сложение определено покомпонентно, то для всех 2-ух чисел a и b:
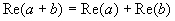
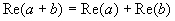
Таковым образом, введенная нами форма скалярной проекции соответствует четвертому свойству скалярного произведения:
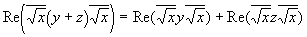
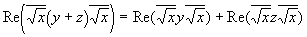
4. Гиперкомплексное произведение как ортогональное преобразование.
В обычном курсе векторной алгебры опосля введения понятия скалярного произведения вводится понятие ортогонального преобразования. Будем следовать классике. Преобразование именуется ортогональным, если скалярное произведение 2-ух векторов равно скалярному произведению их образов опосля преобразования. Обозначив преобразование вектора как F(x), получим:
(F(x),F(y)) = (x,y)
Ортогональным это преобразование именуется из-за того, что если (x,y)=0, то и
(F(x),F(y)) = 0
Другими словами если два вектора были ортогональны, то будут ортогональны и их образы опосля такового преобразования.
ясно, что ортогональное преобразование сохраняет и длину хоть какого вектора:
|F(x)| = |x|
В алгебрах гиперкомплексных чисел одним из видов преобразования является произведение гиперкомплексного числа x на другое гиперкомплексное число a. Покажем, что в случае |a| = 1 такое произведение задает ортогональное преобразование, либо что
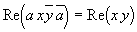
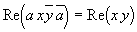
и что при преобразовании
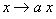
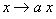
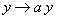
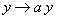
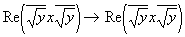
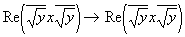
Для этого докажем равенство:
Re(abc) = Re(cab):
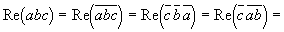
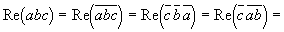
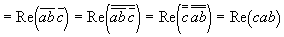
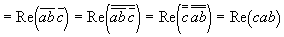
Потому выражение скалярной проекции равно:
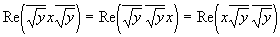
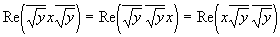
Так как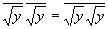 
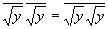
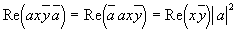
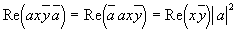
, то получим:
Таковым образом, при задании преобразования числа x как умножения слева на число |a|=1 мы получаем ортогональное преобразование, сохраняющее модуль числа x и скалярную проекцию векторов ax и ay.
То же самое можно обосновать и для умножения справа на число a, где |a|=1.
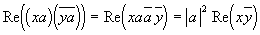
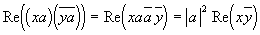
5. Выводы.
Нам удалось отыскать для гиперкомплексных алгебр аналог скалярного произведения, введенного в векторной алшебре. Его удалось отдать в довольно общей форме, распространимой на ассоциативные гиперкомплексные алгебры Кэли — Диксона. Приобретенная форма на сто процентов соответствует четырем главным свойствам скалярного произведения. Проанализировав, в котором конкретно месте рассуждений мы отошли от традиционного варианта, нетрудно найти, что мы нигде не востребовали и не употребляли равенства:
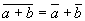
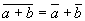
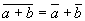
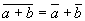
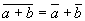
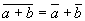
Если б мы востребовали его выполнения, то мы естественным образом сузили бы набор рассматриваемых гиперкомплексных алгебр. Буквально так же, как это было изготовлено в аксиоме Гурвица: Неважно какая нормированная алгебра с единицей изоморфна одной из 4 алгебр — реальных чисел, всеохватывающих чисел, кватернионов либо октав. Наиболее того, равенство у него считается естественным.
Создатель уповает, что некая часть данной статьи может оказаться полезной и при работе с финслеровыми геометриями.
Москва, октябрь 2001.
Перечень литературы
1. И. Л. Кантор, А. С. Солодовников. Гиперкомплексные числа, М, Наука, 1973.
2. Е. А. Каратаев. Скалярно — пространственные повороты в кватернионах, HTTP://karataev.nm.ru/sclvec/index.html
]]>