Учебная работа. Реферат: Организация непрерывных LOD ландшафтов с использованием Адаптивных КвадроДерьев
Введение: в чем неувязка?
Рендеринг ландшафтов является сложной неувязкой при програмировании близкой к реальности графики. В реальный момент мы находимся в увлекательной точке развития технологий рендеринга (т.е. «оцифровки» данных, по которым строится ландшафт), так как увеличившаяся пропускная способность современных графических адаптеров в совокупы с размещенными исследовательскими работами на тему алгоритмов настоящего времени LOD meshing дают возможность современным графическим движкам рисовать очень детализированные ландшафты. Тем не наименее большая часть применяемых технологий дают компромис меж размером ландшафта и его детализированностью.
задачи
Что мы желаем получить от ландшафта? один сплошной меш, начинающийся с заднего плана и продолжающийся до горизонта без разрывов и Т-узлов. Мы желаем созидать огромную область с различной детализацией, начиная от выступов под ногами и заканчивая горами на горизонте. Для определенности скажем, что мы желаем оперировать размерами от 1 метра до 100000 метров с пятью уровнями детализации.
Как этого достигнуть? способ решения в лоб не подойдет для средних компов наших дней. Если мы заведем сетку 100000х100000 16-битных значений, и просто попытаемся ее отрисовать, то получим 2 огромные препядствия. Во-1-х, это препядствия треугольников — мы будет посылать до 20 млн. треугольников на любой кадр. Во-2-х, неувязка памяти — для хранения карты высот нам пригодится примерно 20 Гб памяти. Еще не скоро мы сможем употреблять таковой способ и получать отличные результаты.

Лобовое решение для карты высот.
несколько ранее размещенных способов удачно решают делему треугольников. Более обширно использующиеся — семейство рекурсивных алгоритмов [1], [2], [3] (смотрите в конце перечень литературы). Используя их мы можем расслабленно обработать наш меш и рендерить схожий ландшафт, используя интелектуально избираемые на лету несколько сотен треугольников из 10 милионов.
Тем не наименее, все еще остается неувязка памяти, потому что на хранение карты высот требуется около 20 гб плюс некое количество на метод интелектуального выбора вершин.
Одним из очевидных решений является уменьшение детализации методом роста размера ячейки. 1Kx1K является неплохим фактически применяемым размером карты высот. Не так давно выпущенная игра TreadMarks употребляет набор данных 1k x 1k с прекрасным эффектом [4]. К огорчению, 1k x 1k далековато от 100k x 100k. Итак, мы пришли к компромису меж детализацией фронтального плана и размером ландшафта.
Решение, предлагаемое в данной статье — это употреблять адаптивное квадродерево (quadtree) заместо постоянной сетки для представления инфы о высоте. Используя это квадродерево мы можем закодировать данные с разным разрешение в разных областях. например, в автосимуляторе нам требуется высочайшая детализация дороги и ее окресностей, в эталоне до каждой неровности, но окружающие пустоши, по которым мы не можем двигаться, можно показывать и с наименьшей детализацией. Нам нужна только информация для генерации бугров и долин.
Квадродерево также можно употреблять и для другого подхода к решению препядствия памяти: процедурная детализация. Мысль заключается в том, чтоб определять форму ландшафта на грубом уровне и автоматом генерировать высокодетализированный ландшафт на лету вокруг точки зрения. По адаптивной природе квадродерева все эти сгенерированные детали могут быть отброшены опосля смены точки зрения, таковым образом высвобождая память для сотворения процедурной детализации в другом регионе.
метод: Создание меша
Метод базирован на [1], но также использовались мысли из [2] и [3]. В отличии от [1] существует несколько главных модификаций, но базис этот же самый, потому мы будем придерживатся терминологии [1].
Рендер делится на 2 части: первую называем Update(), а вторую Render(). Во время Update(), мы решаем, какие верхушки включить в выводимый меш. Потом, во время Render() уже генерируем по сиим верхушкам треугольники. Начнем с обычной сетки 3х3 для разъяснения деяния Update() и Render(). Во время Update() мы рассматриваем каждую из необязательных вершин и решаем, включать ли ее в меш. Следуя терминологии [1] мы говорим, что верхушка будет применена в меше и тогда лишь тогда, когда она «включена».
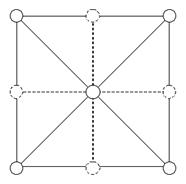

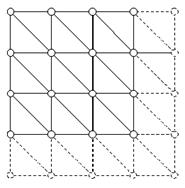
Рис. 2. Сетка 3х3. Пунктирные полосы и верхушки необязательны для LOD ммеша.
Пусть центральная и угловые точки включены (из иерархии выше). Тогда задачка заключается в том, чтоб вычислить для каждой из точек, лежащих на ребрах, ее состояние, руководствуясь некими LOD вычислениями, основанными на точке зрения и параметрах верхушки.
Как мы узнаем, какие из вершин включены, мы можем пользоваться функцией Render(). Это просто — мы составляем веер треугольников (triangle fan) вокруг центральной верхушки, включая каждую включенную верхушку по часовой стрелке. См. рис. 3.
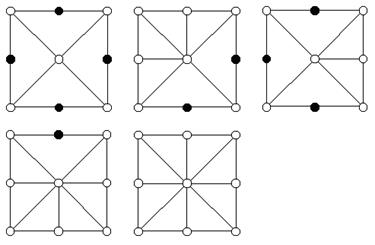

Рис. 3. Сетка 3х3. Выключенные верхушки помечены черным.
Для Update() и Render() адаптивного квадродерева мы повторяем изложенный выше процесс с помощью рекурсивного деления, начиная с сетки 3х3. В процессе деления мы можем получить новейшие верхушки и обрабатываем их также как и верхушки начального квадрата. Но, для того чтоб избежать разрывов, мы руководствуемся несколькими последующими правилами.
Во первых, мы можем поделить всякую комбинацию из 4 квадратов. Когда мы делим квадрант, мы обрабатываем его как подквадрат и включаем его центральную верхушку. Также мы должны включить 2 лежащие на ребрах верхушки родительского квадрата, которые являются углами нашего подквадрата (рис. 4). Другими словами включение подквадрата значит включение его 4 угловых и центальной верхушки.
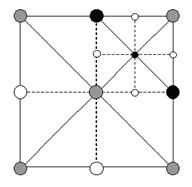

Рис. 4. Деление Северо-Восточного (СВ) квадранта квадрата. Про сервые верхушки мы уже знаем что они включены, но темные врубаются в итоге деления квадрата.
Но, не считая того, верхушка, лежащая на ребре подквадрата, является общей для примыкающего подквадрата. Таковым образом, когда мы включаем реберную верхушку, нужно удостоверится что и в примыкающем подквадрате она тоже включена. Включение ее в примыкающем квадрате может, в свою очередь, включить ее у нас, т.е. флаг включения должны передаватся через квадродерево. синхронизация этих флагов у примыкающих квадратов нужна для обеспечения целосности меша. См. [1] для неплохого описания правил зависимости включения.
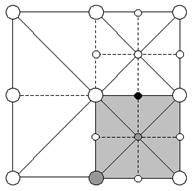

Рис. 5. Во время Update() для NE квадранта мы принимаем решение включить черную верхушку. Потому что эта верхушка общая с SE квадрантов (помеченным сероватым), то мы должны включить этот квадрант тоже. Включение SE вкадранта в свою очередь принудит нас включить помеченные сероватым верхушки.
Опосля того как мы закончим с Update() мы можем вызвать Render(). Рендер весьма прост — все вычисления по сохранению целостности меша уже были выполнены в Update(). Мысль, на которой основан Render() — это рекурсивный вызов Render для включенных подквадратов и потом отрисовка всех треугольников квадрата, которые не были покрыты включенными подквадратами.
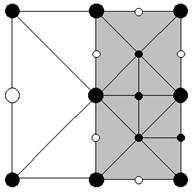

Рис 6. Пример меша. Включенные верхушки помечены черным. Сероватые треугольники отрисованы во время рекурсивного вызова Render() для сопоставленных им подквадратов. Белоснежные треугольники отрисоввываются во время изначального вызова Render() для этого квадрата.
метод: Обработка вершин и квадратов
Перейдем к самому вычислению — обязана ли верхушка быть включена. Для этого существует несколько способов. Все, которые я принял во внимание, именуются «vertex interpolation error» (ошибка интерполяции верхушки), либо, короче, vertex error. Это разница меж высотой верхушки и высотой ребра в треугольнике, который апроксимирует верхушку, когда та выключена (Рис. 7). Верхушки с большей ошибкой должны быть лучше вершин с малеханькой ошибкой. иной вариант основан на растоянии верхушки от точки зрения. Интуитивно, имея 2 верхушки с схожей ошибкой мы должны избрать наиболее ближнюю.
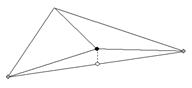

Рис. 7. Vertex interpolation error. Когда верхушка включена либо выключена, меш меняяет форму. Наибольшее изменение, получающееся при включении верхушки показано пунктирной линией. Величина конфигурации есть разница меж настоящей высотой верхушки (темная точка) и высотой ребра под ним (белоснежная точка). Белоснежная точка — это просто середина меж 2 сероватыми точками. (Wolverene: Середина — потому что мы рассматриваем измельчающиеся квадраты в quadtree и точка деления лежит ровно в центре).
Также есть остальные действующие причины. например, в [1] принимается во внимание направление меж верхушкой и точкой зрения. Мысль заключается в screen space error (экранной ошибке) — интуитивно vertex error наименее видима чем наиболее вертикально данное направление. В [1] описана вся эта математика в деталях.
Но я не думаю что screen space error является неплохой метрикой по двум причинам: во-1-х, он игнорирует текстурную перспективу и depth buffering errors — даже если верхушка не движется на дисплее, т.к. она двигается строго пенпердикулярно к/от точки зрения, Z прямо вниз является как легким случаем для LOD ландшафтов, так и не обычным случаем.
На мой взор, нет смысла улучшить для нетипичного легкого варианта. Вариант, когда ось зрения наиболее горизонтальна и большая часть ландшафта видима описывает меньший framerate, и, как следует, эффективность метода.
Заместо screen-space geometric error я предлагаю созодать схожий тест в трехмерном пространстве с ошибкой пропорциональной дистанции. Он включает лишь 3 величины: L1 норму вектора меж верхушкой и точкой зрения, vertex error и постоянный «порог детализации»(Threshold).
Vertex test:
L1 = max(абс(vertx — viewx), абс(verty — viewy), абс(vertz — viewz));
enabled = error * Threshold < L1;
На практике внедрение L1 нормы значит огромную глубину делений вдоль диагоналей горизонтальной плоскости ландшафта. Я не сумел увидеть данный эффект глазом, так что я не думаю что о этом стоит волноваться. [4] и остальные употребляют view-space-z заместо L1 нормы, что на теоретическом уровне является даже наиболее правильным чем настоящая дистанция меж верхушкой и точкой зрения. Невзирая на это, L1 по-моему работает лучшим образом и в [3] она тоже употребляется.
Можно употреблять Threshold как регулятор подстройки скорость/свойство, но он не имеет точной геометричесой интерпретации. Грубо говоря, он значит: для данного растояния z, худшей ошибкой с которой я буду мирится будет z / Threshold. естественно, вы сможете произвести некие вычисления угла зрения и связать Threshold с наибольшей пиксельной ошибкой, но я никогда не разглядывал его наиболее чем
Вот так работает включение вершин. Но что является наиболее принципиальным, как работает включение подквадратов во время Update()? Ответом является box test. Он задает последующий вопросец: рассматриваем выровненный по осям 3D Box, содержащий участок ландшафта (т.е. элемент quadtree), и знаем соответвующую ему наивысшую vertex error всех вершин снутри. Может ли vertex enable test возвратить истин для какой-нибудь верхушки из этого квадрата? Если да, то делим.
Красота этого способа в том, что делая BoxTest мы можем одним ударом отсечь тыщи вершин. Это делает Update() вполне масштабируемым: стоимость его не зависит от размера всего набора данных, а только от размера данных, включенных в текущий LOD меш. И, как побочное явление, предпросчитанный вертикальный размер Bounding Box может использоватся для frustim culling. (примечание wolverene — координаты x и z мы уже знаем из выбора квадрата как элемента quadtree, т.е. для построения BoundBox нам нужно знать только вертикальный его размер).
Box Test консервативен в том смысле что верхушка, из-за которой Box Test возвратил «Да» (т.е. необходимость деления) может находится на иной стороне bound box от ближней к точке зрения стороны bound box, и, таковым образом, сама верхушка может этот тест провалить. Но на самом деле это не тянет огромных затратных расходов — несколько box test и vertex test.
Box test имеет последующий вид, весьма схожий на VertexTest:
Box test:
bc[x,y,z] == coordinates of box center
ex[x,y,z] == extent of box from the center (i.e. 1/2 the box dimensions)
L1 = max(абс(bcx — viewx) — exx, абс(bcy — viewy) — exy, абс(bcz — viewz) — exz)
enabled = maxerror * Threshold < L1
Индивидуальности
:
Детали
В прошлом разделе была описана сущность метода, но оставлена в стороне маса деталей, некие из которых являются главными. Во-1-х, где, фактически хранится информация о высоте? В прошлых методах была постоянная сетка высот, на которой неявно [1] & [3] либо очевидно [3] определялся меш. Главной инновацией в моем способе будет то, что данные хранятся фактически в адаптивном quadtree. В итоге получаем 2 главные выгоды. Во-1-х, данные размещаются адаптивно в согласовании с той их частью, что нужна приложению; таковым образом наименьшее количество данных относится к сглаженной части ландшафта, в какой не предполагается нахождение камеры. Во-2-х, дерево может динамически расти либо уменьшатся зависимо от нахождения точки зрения наблюдающего; процедурная детализация быть может добавлена на лету в регионе, в каком находится камера и потом удалена, как камера покинет данный регион.
Для того, чтоб хранить информацию о высотах любой элемент quadtree должен хранить информацию о высоте собственной центральной верхушки и по последней мере 2-ух вершин, лежащих на ребрах. Все остальные высоты хранятся в примыкающих узлах дерева. например, высота угловых вершин приходит из родительского квадрата и его соседей. Оставшиеся высоты реберных верших хранятся в примыкающих квадратах. В текущей реализации я храню высоту центральной верхушки и все 4 высоты реберных вершин. Это упрощает работу за счет того, что нужные для обработки квадрата данные доступны как данные квадрата либо характеристики функции. Недочетом будет то, что любая реберная точка хранится к дереве два раза.
Так же в текущей реализации одно и то же quadtree употребляется для хранения высоты и для построения меша. Совершенно-то отлично бы его поделить на 2 — одно для хранения карты высот, 2-ое для построения меша. Потенциальные красоты такового подхода изложены ниже.
Большая часть трюков реализации основано на общих для 2-ух примыкающих квадратов реберных вершин. например, таковой вопросец — какой квадрат должен делать vertex-enable test для реберной верхушки? Мой ответ — любой квадрат инспектирует лишь свои южную и восточную реберные верхушки и полагается на проверки северного и западного соседа для проверки 2-ух остальных вершин.
иной интерестный вопросец — нужно ли нам сбрасывать все флаги перед Update() либо же продолжать с состоянием, оставшимся от предшествующего цикла отрисовки? Мой ответ — продолжаем работу от предшествующего состояния, как в [2], но не как в [1] и [4]. Это ведет к большей детализированности — мы инспектировали условия на включение, но когда мы можем выключить верхушку либо квадрат? Как мы помним из метода Update() включение верхушки принуждает включится зависящие от нее верхушки, и так дальше по дереву. Мы не можем просто так выключить верхушку посреди одной из таковых цепей зависимостей, если верхушка зависит от какой-нибудь иной включенной верхушки. По другому у нас получатся разрывы в меше, или принципиальные включенные верхушки не будут отрисованы.
На рис. 8 видно что реберная верхушка имеет 4 примыкающих квадрата, которые употребляют ее как угловую верхушку. Если хоть какой из этих подквадратов включен, то обязана быть включена данная верхушка. Так как квадрат включен когда центральная его верхушка включена, то одним из подходов будет проверить все примыкающие подквадраты перед отключением. Тем не наименее, в моей реализации это будет очень тяжело, потому что для нахождения примыкающих квадратов придется обегать ве дерево. Заместо этого я считаю число ссылок для каждой реберной верхушки. Оно равно числу подквадратов, от 0 до 4, которые включены. Это значит что всякий раз когда мы включаем/выключаем квадрат, мы должны обновить число ссылок в 2-ух верхушках. К Счастью, число ссылок изменяется от 0 до 4, т.е. все это можно запаковать в 3 бита.
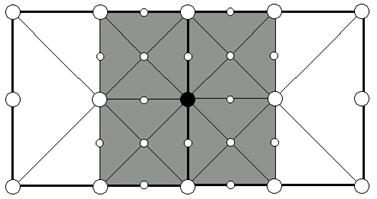

Рис. 8. Любая реберная верхушка имеет 4 примыкающих подквадрата, которые употребляют ее как угловую. Если хоть какой из этих квадратов включен, то и верхушка обязана быть включена. например, темная верхушка обязана быть включена если включен один из сероватых квадратов.
Таковым образом выключающий тест весьма прост: если верхушка включена, число ссылок равно 0 и vertex test для текущей точки камеры возвращает false, выключаем верхушку. По другому не трогаем ее. Условия выключения квадрата тоже достаточно прямолинейны: если квадрат включен и он не корень дерева, и нет включеных реберных вершин и нет включеных подквадратов, квадрат проваливает BoxTest, выключаем его.
Индивидуальности: память
Весьма принципиальной чертой этого либо хоть какого другого LOD способа является потребление памяти. В полном quadtree один квадрат эквивалентен трем верхушкам обыкновенной сетки высот, так что требуется создать структуру квадрата как можно компактнее. К Счастью, Render() и Update() способы не требуют от всякого квадрата инфы по всем 9 верхушкам. Вот перечень требуемых данных:
· 5 высот (углы и центр)
· 6 значений ошибок (верхушки на восточном и южном ребрах и 4 подквадрата)
· 2 счетчика включенных подквадратов (для вершин на восточном и южном ребрах)
· 8 1-битовых флагов включения (по 1 для каждой верхушки и всякого подквадрата)
· 4 указателя на подквадраты
· 2 значения высоты для малого/наибольшего вертикального размера
· 1 1-битный флаг, показывающий что этот квадрат не быть может удален.
Зависимо от нужд приложения значения высот могут быть уютно упакованы в 8 либо 16 бит. Значения ошибок могут употреблять этот же самый формат, но, используя нелинейное сжатие вы сможете запаковать их еще больше. Все счетчики ссылок и статистический флаг поместятся в 1 б. Флаги включения тоже пакуются в 1 б. Размер указателей на подквадраты зависит от наибольшего числа узлов, которые могут быть применены. Обычно это сотки либо тыщи, так что я использую 20 бит на любой указатель как минимум. Малое и наибольшее значения высоты тоже могут быть сжаты разными методами, но 8 бит на любой смотрится разумным минимумом. Все вкупе это занимает 191 бит (24 б) на квадрат при 8-битных значениях высоты. 16-битные значения высот требуют 29 байтов. 32-байтный размер размер квадрата смотрится неплохой целью для бережливой реализации. 36 байтов я обязан употреблять, потому что я не пробовал упаковывать указатели на подквадраты. иной трюк — употреблять фиксированный массив с подменой алокаторов для quadsquare::new и quadsquare::delete. Это сжимает 4 б затратных расходов обычного для С++ аллокатора (как я предполагаю) до 1 бита.
Существует много трюов и схем компресии для того чтоб сжать данные еще посильнее, но они наращивают сложность и уменьшают производительность. В любом случае, 36 байтов на 3 верхушки не совершенно плохо. Это 12 байтов на верхушку. В [1] было достигнуто 6 байтов на верхушку.
С одной стороны это весьма много, но с иной стороны адаптивная структура quadtree дозволяет хранить разреженные данные в ровненьких областях либо областях, для которых не требуется высочайшая детализация. В то же время в высоко принципиальных областях можно добиться высочайшей детализации; например, в той же игре-автосимуляторе можно хранить даже выпуклости и рытвины на дороге.
Индивидуальности: Геоморфинг
[2] и [3] также употребляют морфинг вершин либо, по другому, геоморфинг. Мысль в том, что при включении вершин получаются резкие скачки меж предшествующим мешом, в каком данная верхушка была отключена и отрисованным в данном кадре, в каком верхушка была включена. Для того, чтоб избавится от этого эффекта применяется плавная анимация из интерполированного положения верхушки в ее истинное
К несчастью, выполнение геоморфинга просит хранения еще 1-го значения высоты для анимируемой верхушки, что представляет собой настоящую делему для метода адаптивных quadtre в той его реализации, которая была описана. Будет нужно несколько доп байтов на каждую верхушку, что не так просто. В [3] такие данные хранятся на каждую верхушку, но в [2] этого стараются избежать, потому что на самом деле доп значения высоты обязано хранится только для верхушки, которая включена в данный меш, но не для всего набора данных.
Есть три суждения по поводу геоморфинга. 1-ый подход — издержать доп память на хранение доп значения высоты для всякого меша. 2-ой кандидатурой является сделать лучше метод так, чтоб добиться вправду относительно малеханьких ошибок, т.е. геоморфность просто не будет нужно. К тому же согласно закону Мура возможно это скоро будет реализовываться на уровне hardware. Третьей кандидатурой является поделить quadtree на 2 дерева: одно для хранения данных (дерево высот), 2-ое для хранения отображаемого меша (дерево меша). В дереве высот будут хранится все высоты и предпросчитанные ошибки, но ничего из временных данных, таковых как флаги включения, число ссылок, веса морфинга и так дальше. При построении дерева меша можно не задумыватся о ограничениях памяти, так как его размер пропорционален числу деталей, отрисовывающихся в данный момент. В то же время дерево высот может сохранить мало памяти, потому что оно является статическим и, таковым образом, из него можно удалить огромное количество ссылок на малышей.
Не считая того таковая теория в дополнение к уменьшения требуемой памяти может увелить локальность данных и сделать лучше внедрение кэша методом.
Приложения
Работающая реализация
Графический движок Soul Rider является закрытым и навряд ли будет открыт в обозримом будущем, но я переписал базы метода в качестве демонстрации для данной статьи. Эти исходники могут быть свободно применены для исследования, тестов, модификации и включения в ваш свой коммерческий/некоммерческий проект. Я только прошу упомянуть меня.
Я не употреблял никаких запаковок данных в демо-коде. Это отменная область для тестов. Также я не употреблял отсечение по пирамиде видимости, но все нужные данные доступны.
Упражнения для читателя
В дополнение к запаковке данных упомяну о неких остальных вещах, включенных в движок Soul Ride, но не включенных в демо. одной из огромных является однозначная-полноландшафтная система текстурирования (wolverene: наверняка, имеется ввиду что на весь ландшафт накладывается 1 текстура), описание которой выходит за рамки данной статьи.
иной вещью, с которой я не эксперементировал, но которую просто осознать по демо-коду — это процедурная детализация по запросу. По-моему, это одно из многообещающих направлений развития компьютерной графики. Просто не видно другого метода хранить и моделировать виртуальные миры в деталях достаточных для заслуги богатства отображения настоящего мира. Я думаю что метод quadtree в силу его масштабируемости быть может полезен для программистов, работающих над процедурной детализацией.
Иным полезным решением является подкачка по запросу подсекций дерева. На самом деле это не так трудно: просто следует завести особый флаг для определенных подквадратов; в их будет содержаться ссылка на все гиганское поддерево, хранящееся на диске с просчитанной и лежащей в обыкновенном дереве наибольшей ошибкой. Когда Update() старается включить «особый» квадрат, последует пауза, подкачка данного квадрата с диска и подключение его в дерево, а потом возобновление работы Update(). Реализация этого в фоновом режиме без задержек была бы еще интерестнее, но я думаю, выполнима. В итоге получим нескончаемую подкачку. Процедурная детализация по запросу базирована на той же самой идее: заместо того, чтоб забивать диск предподготовленными данными, вы просто запускаете метод роста детализации на лету.
И еще одной увлекательной работой было бы обнаружение узеньких мест в методе.
Перечень
литературы
[1] Peter Lindstrom, David Koller, William Ribarsky, Larry F. Hodges, Nick Faust and Gregory A. Turner. «Real-Time, Continuous Level of Detail Rendering of Height Fields». In SIGGRAPH 96 Conference Proceedings, pp. 109-118, Aug 1996.
[2] Mark Duchaineau, Murray Wolinski, David E. Sigeti, Mark C. Miller, Charles Aldrich and Mark B. Mineev-Weinstein. «ROAMing Terrain: Real-time, Optimally Adapting Meshes.» Proceedings of the Conference on Visualization ’97, pp. 81-88, Oct 1997.
[3] Stefan Rцttger, Wolfgang Heidrich, Philipp Slusallek, Hans-Peter Seidel. Real-Time Generation of Continuous Levels of Detail for Height Fields. Technical Report 13/1997, Universitдt Erlangen-Nьrnberg.
[4] Seumas McNally. HTTP://www.longbowdigitalarts.com/seumas/progbintri.html This is a good practical introduction to Binary Triangle Trees from [2]. Also see HTTP://www.treadmarks.com/, a game which uses methods from [2].
[5] Ben Discoe, HTTP://www.vterrain.org/ . This web site is an excellent survey of algorithms, implementations, tools and techniques related to terrain rendering.
]]>
