Учебная работа. Реферат: Интегральное исчисление. Исторический очерк
понятие интеграл конкретно соединено с интегральным исчислением – разделом арифметики, занимающимся исследованием интегралов, их параметров и способов вычисления. вкупе с дифференциальным исчислением интегральное исчисление составляет базу математического анализа.
Истоки интегрального исчисления относятся к древнему периоду развития арифметики и берут начало от способа исчерпывания, разработанного математиками Старой Греции.
способ исчерпывания это набор правил для вычисления площадей и объёмов, разработка которых приписывается Евдоксу Книдскому. Предстоящее развитие способ получил в работах Евклида, а особенным искусством и многообразием внедрения способа исчерпывания славился Архимед.
Обычная схема доказательств способом исчерпывания смотрелась последующим образом. Для определения величины A строилась некая последовательность величин С1, С2, …, Сn, … таковая, что
Предполагалось также известным такое B, что
и что для хоть какого целого K можно отыскать довольно огромное n, удовлетворяющее условию:
Где D – повсевременно. Опосля массивных рассуждений из крайнего выражения удавалось получить:
Как видно из приведённой схемы способ был основан на аппроксимации рассматриваемых объектов ступенчатыми фигурами либо телами, составленными из простых фигур либо пространственных тел (прямоугольников, параллелепипедов, цилиндров и т.п., обозначенных последовательностью С1, С2, …, Сn, …). В этом смысле способ исчерпывания можно разглядывать как древний интегральный способ.
Кризис и упадок старого мира привёл к забвению почти всех научных достижений. О способе исчерпывания вспомянули только в XVII веке. Это было соединено с именами Исаака Ньютона , Готфрида Лейбница, Леонарда Эйлера и ряда остальных выдающихся учёных, положивших базу современного математического анализа.
В конце XVII и в XVIII веке все растущие запросы практики и остальных наук вдохновляли ученых очень расширять область и способы исследовательских работ арифметики. Понятия бесконечности, движения и многофункциональной зависимости выдвигаются на 1-ое пространство, стают основой новейших способов арифметики.
В конце XVII и в XVIII веке в арифметике и механике были получены традиционные результаты фундаментального значения. Главным тут было развитие дифференциального и интегрального исчисления, теории дифференциальных уравнений, вариационного исчисления и аналитической механики.
Главные понятия и теория интегрального и дифференциального исчислений, до этого всего связь операций дифференцирования и интегрирования, также их внедрения к решению прикладных задач были разработаны в конце XVII века, но основывались на идеях, сформулированных сначала XVII веке величавым математиком и астрологом Иоганом Кеплером.
В ноябре 1613 года царский математик и астроном австрийского двора И. Кеплер праздновал женитьбу. Готовясь к ней, он приобрёл несколько бочек виноградового вина. При покупке Кеплер был поражён тем, что торговец определял вместимость бочки, производя одно единственное действие — измеряя расстояние от наливного отверстия до самой далекой от него точки днища. Ведь такое измерение совсем не учитывало форму бочки! Кеплер сходу узрел, что перед ним наинтереснейшая математическая задачка — по нескольким измерениям вычислить вместимость бочки. Размышляя над данной нам задачей, он нашёл формулы не только лишь для объёма бочек, да и для объёма самых разных тел: лимона, яблока, айвы и даже турецкой чалмы. Для всякого из тел Кеплеру приходилось создавать новейшие, часто весьма хитроумные способы, что было очень неловко. Попытка отыскать довольно общие, а, основное, обыкновенные способы решения схожих задач и привела к появлению современного интегрального счисления. Но это уже была награда совершенно другого математика.
Тяжело отыскать другое имя, которое оказало бы настолько мощное воздействие на историю мировой науки и культуры, как Исаак Ньютон. Узнаваемый математик и историк науки Б. Л. Ван-дер-Варден пишет в собственной книжке “Пробуждающаяся наука”: “Любой естествоиспытатель непременно согласится, что механика Ньютона есть база современной физики. Любой астролог понимает, что современная астрономия начинается с Кеплера и Ньютона. И любой математик понимает, что самим значимым н более принципиальным для физики отделом современной арифметики является анализ, в базе которого лежат дифференциальное и интегральное исчисления Ньютона. Как следует, труды Ньютона являются основой большой части четких наук нашего времени”. И не только лишь наук: “Математика и техника влияют даже на нашу духовную жизнь, и так. что мы изредка можем представить это для себя на сто процентов. Вослед за неестественным взлётом, которое пережило и XVII веке естествознание, последовал безизбежно рационализм XVIII века, обожествление разума, упадок религии… Кто дает для себя отчет в том, — спрашивает создатель, — что с исторической точки зрения Ньютон является самой значимой фигурой XVII века?”
Исаак Ньютон родился в 1643 году. Мальчишка посещал поначалу сельскую школу, а в двенадцать лет его выслали обучаться в ближний город. Директор школы направил внимание на способного мальчугана и уговорил мама Ньютона выслать отпрыска обучаться в Кембриджский институт. Ньютон был принят туда в качестве бедного студента, обязанного прислуживать бакалаврам, магистрам и студентам старших курсов.
Кафедру арифметике в Кембридже занимал тогда юный блестящий учёный Исаак Барроу. Он скоро стал не только лишь учителем, да и другом Ньютона, а спустя несколько лет уступил собственному величавому ученику кафедру арифметики. К этому времени Ньютон получил уже степени бакалавра и магистра. В 1665-1667 годах Ньютон начал работать над созданием математического аппарата, при помощи которого можно было бы изучить и выражать законы физики. Ньютон 1-ый выстроил дифференциальное и интегральное исчисления (он именовал его способом флюксий). Это сходу позволило решать самые различные, математические и физические, задачки. До Ньютона почти все функции определялись лишь геометрически, так что к ним нереально было использовать алгебру и новое исчисление флюксий. Ньютон отыскал новейший общий способ аналитического представления функции — он ввел в арифметику и начал систематически использовать нескончаемые ряды.
Поясним эту идею Ньютона. Понятно, что хоть какое действительное число можно представить десятичной дробью — конечной либо нескончаемой. Так. к примеру:
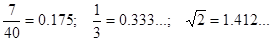
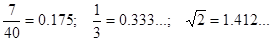
Это означает, что хоть какое число a можно представить в виде:
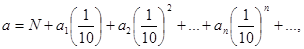
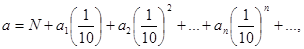
где N — целая часть, а a1, a2, … an, … могут принимать одно из значений 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. По аналогии с таковым представлением чисел Ньютон представил, что неважно какая функция от x, к примеру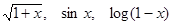 
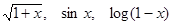
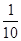
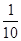
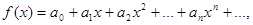
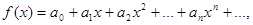
, быть может представлена как нескончаемый многочлен либо ряд, расположенный уже не по степеням 
, а по степеням x:
где a1, a2, … an, …- коэффициенты, которые всякий раз должны быть определены. Примером такового ряда может служить популярная нам геометрическая прогрессия:
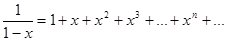
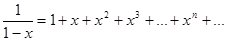
сразу с Ньютоном к аналогичным идеям пришел иной выдающийся учёный — Готфрид Вильгельм Лейбниц.
Готфрид Вильгельм Лейбниц родился в Германии в г. Лейпциге в 1646 г. Пытливый мальчишка уже 6 лет вел достойные внимания беседы по истории со своим папой, доктором Лейпцигского института. К 12 годам он отлично исследовал латинский язык и увлёкся древнегреческим. В особенности его заинтересовывали древнейшие философы, и он мог длительно размышлять о философских теориях Аристотеля либо Демокрита. В 15 лет Лейбниц поступает и Лейпцигский институт, где усердно изучает Право и философию. Он весьма много читает, посреди его возлюбленных книжек — книжки Р. Декарта, Г. Галилея, II. Кеплера и Д. Кампанеллы.
Свои колоссальные познания но арифметике Лейбниц заполучил самоучкой. Через три года, закончив институт, Лейбниц покинул Лейпциг. Он был обижен отказом ученого совета института присвоить ому степень доктора прав. Отказ растолковали тем. что Лейбниц был… очень молод!
Началась жизнь, полная напряженного труда и бессчетных путешествии. Просто для себя представить, как неудобны были путешествовать в неловких каретах по тряским дорогам Европы тех времен. Лейбниц умел не терять времени даром — много успешных мыслей пришло ему и голову конкретно во время этих длительных поездок. Лейбниц различался исключительной способностью стремительно “заходить” и задачку и решать ее более общим методом. Размышляя над философскими и математическими вопросцами, Лейбниц удостоверился, что самым надежным средством находить и отыскивать истин в науке может стать математика. Всю спою сознательную жизнь он стремился выразить законы мышления, людскую способность мыслить и виде математического исчисления. Для этого нужно, учил Лейбниц, уметь обозначать любые понятия либо идеи определенными знаками, сочитая их в особенные формулы, и сводить правила мышления к правилам в вычислениях но сиим символическим формулам. Заменяя oбычные слова верно определенными знаками, Лейбниц стремился освободить наши рассуждения от всякой неопределенности и способности ошибиться самому либо вводить в заблуждение остальных. Если, грезил Лейбниц. меж людьми возникнут разногласия, то решаться они будут не в длинноватых и мучительных спорах. а так, как решаются задачки либо доказываются аксиомы. Спорщики возьмут в руки перья и, сказав: “Начнем вычислять” — примутся за расчеты.
Как уже отмечалось, Лейбниц сразу с Ньютоном и независимо от него открыл главные принципы дифференциального и интегрального исчислений. Теория заполучила силу опосля того, как Лейбницем и Ньютоном было подтверждено, что дифференцирование и интегрирование — взаимно оборотные операции. О этом свойстве хороню знал и Ньютон. Но лишь Лейбниц узрел тут ту восхитительную возможность, которую открывает применение символического способа.
Хоть какой человек, исследовав маленькое число правил деяния с знаками, обозначающими операции дифференцирования и интегрирования, становится владельцем массивного математического способа. В наше время такие знаки операций именуют операторами. Операторы дифференцирования d( ) и интегрирования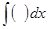 
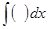
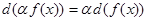
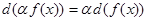
действуют на функции, “перерабатывая” их в остальные, буквально вычисляемые функции. Лейбниц разрабатывает необыкновенную алгебру действий с этими операторами. Он обосновывает, что обыденное число а можно выносить за символ оператора:
Схожие операторы можно выносить за скобку:
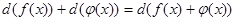
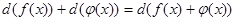
либо:
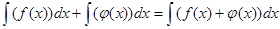
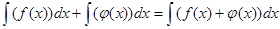
Сокращенно все перечисленные характеристики можно выразить соотношением:
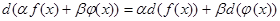
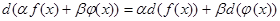
где: a и b — числа.
Операторы. которые владеют таковым свойством. именуются линейными. Теория линейных операторов, которую с таковым фуррором начал развивать, Лейбниц,. в современной арифметике является отлично разработанной и полезной в приложениях теорией.
Неоднократное применение операторов можно принимать как степень оператора, к примеру, для d( ):
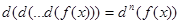
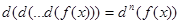
То, что главные операторы математического анализа являются взаимно оборотными Лейбниц подчёркивал собственной символикой, утверждая, что в d(x) и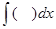 
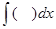
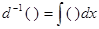
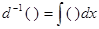
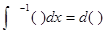
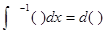
также взаимно обратны, как степени и корешки в обыкновенном исчислении. Употребляя так же обозначение, аналогичное обозначению a-1 числа, оборотного a, причём произведение a×a-1=1. Обозначая операторы 
либо напротив:
и понимая под их произведением последовательное их применение, имеем:
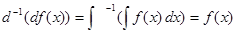
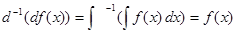
т. е. произведение есть “единица”, не меняющая функцию.
Но, в подходе Ньютона-Лейбница крылось серьёзное противоречие.
Лейбниц и его последователи — братья Бернулли, Лопиталь и остальные — трактовали дифференциалы как нескончаемо малые разности обыденных конечных величин, как тогда гласили — “настоящих” величин “низшей” арифметики. Потому они обращались с теми и иными идиентично и в исчислении применяли к первым те же приемы, которые справедливы при действиях со вторыми. вкупе с тем выяснилось, что таковым образом трактуемым нескончаемо малым присуще свойство, противоречащее одному основному свойству главных конечных величин: если А — конечная величина, а a — нескончаемо малая, то, чтоб итог исчисления выходил совсем четким, оказалось нужным проводить вычисления в предположении, что А+a=А.
Дифференциальное исчисление, способами получить четкий итог, было надо исходить из неверного утверждения.
Ньютон пробовал доказать дифференциальное исчисление на законах механики и понятии предела. Но ему не удалось высвободить свое исчисление флюксий от недочетов, присущих дифференциальному исчислению Лейбница. В практике вычисления Ньютон, как и Лейбниц, использовал принцип отбрасывания нескончаемо малых.
Таковая непоследовательность дозволила именовать дифференциальное исчисление Лейбница–Ньютона магическим. Сиим сначала подчеркивалось, что Лейбниц и Ньютон вводили в дифференциальное исчисление нескончаемо малые величины метафизически, сходу полагая их существующими, без выяснения их появления и развития и без анализа природы их специфичных параметров.
Пробы выстроить анализ нескончаемо малых и теорию рядов в полном согласовании с главными понятиями и правдами “низшей” арифметики с самого начала к удачным результатам не привели. Потому Лейбниц и его последователи пробовали оправдать принципы анализа нескончаемо малых методом сопоставления нескончаемо малой с песчинкой, которой можно пренебречь при вычислении высоты горы, средством ссылок на возможность и т. п.
Иная попытка была предпринята в конце XVIII века. Узнаваемый германский математик Вессель предложил бросить анализ нескончаемо малых в анализе в качестве “нужных вспомогательных функций”. Но, таковая трактовка широкого распространения не получила — арифметики знали механическое и геометрическое толкование dx и dy.
Приблизительно с крайней четверти XVIII века область приложений математического анализа начинает существенно перекрывать границы его обыденного приложения в механике и геометрии. Ещё резвее развертывается этот процесс в первой четверти XIX века.
Арифметики пробовали поначалу решать новейшие задачки способами, разработанными классиками XVIII века — Эйлером, Даламбером, Лагранжем и иными. Но, скоро выяснилось, что способы классиков недостаточны, что нужно развивать новейшие, наиболее общие и мощные способы. Выяснилось также, что дефицитность способов классиков часто связана с узостью трактовки главных понятий, с “изгоняемым” понятием о нескончаемо малом, с “исключениями”, которые ранее оставались в тени.
Поясним произнесенное одним примером.
Ньютон и Лейбниц разработали две трактовки понятия обыденного определенного интеграла.
Ньютон трактовал определенный интеграл как разность соответственных значений первообразной функции:
,
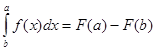
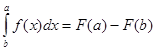
где F`(x)=f(x).
Для Лейбница определенный интеграл был суммой всех нескончаемо малых дифференциалов.
.
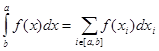
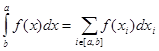
1-ая трактовка отвечала технике вычисления определенных интегралов с помощью первообразной подынтегральной функции, 2-ая — поэтому, что в приложениях определенный интеграл возникал как предел известного вида суммы (интегральной суммы).
Приблизительно до крайней четверти XVIII века 1-ая трактовка понятия определенного интеграла занимала господствующее положение. Этому содействовали два происшествия.
К началу XVIII века были установлены правила дифференцирования всех простых функций и началась удачная разработка способов нахождения их первообразных (оптимальных, отдельных классов иррациональных и непознаваемых функций). Благодаря этому точка зрения Ньютона полностью отвечала развитию действенных алгоритмов интегрального исчисления.
Конкретное вычисление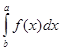 
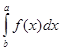
как предела интегральной суммы столкнулось с почти всеми трудностями. естественно, что это событие укреплению точки зрения Лейбница не содействовало.
Толкование обыденного определенного интеграла по Лейбницу опиралось на понятие о нескончаемо малых, от которого арифметики XVIII века желали высвободить математический анализ. Это также содействовало укреплению точки зрения Ньютона. Факт этот отлично подтверждался тем, как Леонард Эйлер употреблял понятие о интегральной сумме. Эйлер не возражал против приближенного вычисления определенных интегралов с помощью соответственных интегральных сумм. Но разглядывать определенный интеграл как предел интегральной суммы он не мог. В этом случае все слагаемые интегральной суммы становились нескончаемо малыми, т. е., исходя из убеждений Эйлера, были нулями.
Историческая справка. В 1963 г. 23-летний Пауль Эйлер закончил курс теологии в Базельском институте. Но учёных теологов было в те годы больше, чем требовалось, и только в 1701 г. он получил официальную должность священника сиротского дома в Базеле. 19 апреля 1706 г. пастор Пауль Эйлер женился на дочери священника. А 15 апреля 1707 г. у их родился отпрыск, нареченный Леонардом.
Изначальное обучение будущий учёный прошел дома под управлением отца, учившегося некогда арифметике у Якоба Бернулли. Хороший пастор готовил старшего отпрыска к духовной карьере, но занимался с ним и арифметикой – как в качестве утехи, так и для развития логического мышления. Мальчишка увлёкся арифметикой, стал задавать папе вопросцы один труднее другого.
Когда у Леонардо проявился Энтузиазм к учёбе, его направили в Базельскую латинскую гимназию – под надзор бабушки.
20 октября 1720 г. 13-летний Леонард Эйлер стал студентом факультета искусств Базельского института: отец желал, чтоб он стал священником. Но любовь к арифметике, блестящая память и хорошая работоспособность отпрыска изменили эти намерения и направили Леонарда по иному пути.
Став студентом, он просто усваивал учебные предметы, отдавая предпочтение арифметике. И нехитро, что способный мальчишка скоро направил на себя внимание Бернулли. Он предложил юноше читать математические воспоминания, а по субботам приходить к нему домой, чтоб вместе разбирать непонятное. В доме собственного учителя Эйлер познакомился и сдружился с отпрысками Бернулли – Николаем и Даниилом, также увлечённо занимавшимися арифметикой. А 8 июня 1724г. 17-летний Леонард Эйлер произнёс по- латыни прекрасную речь о сопоставлении философских мнений Декарта и Ньютона — и был удостоен учёной степени магистра (в XIX в. в большинстве институтов Западной Европы ученая степень магистра была заменена степенью доктора философии).
Эйлер различался феноменальной работоспособностью. Он просто не мог не заниматься арифметикой либо её приложениями. В 1735 г. Академия получила задание выполнить срочное и весьма громоздкое астрономическое вычисление. Группа академиков просила на эту работу три месяца, а Эйлер взялся выполнить работу за 3 денька – и совладал без помощи других. Но перенапряжение не прошло безо всяких следов: он захворал и растерял зрение на правый глаз. Но учёный отнёсся к несчастью с величайшим спокойствием: “Сейчас я меньше буду отвлекаться от занятий арифметикой”, — философски увидел он.
Ранее времени Эйлер был известен только узенькому кругу учёных. Но двухтомное сочинение “ Механика, либо наука о движении, в аналитическом изложении ”, изданное в 1736 г., принесло ему мировую славу. Эйлер искрометно применил способы математического анализа к решению заморочек движения в пустоте и в сопротивляющейся среде. “Тот , кто имеет достаточные способности в анализе, сумеет всё узреть с необыкновенной лёгкостью и без всякой помощи прочтет работу на сто процентов”, — кончает Эйлер своё вступление к книжке.
Дух времени добивался аналитического пути развития четких наук, внедрения дифференциального и интегрального исчисления для описания физических явлений. Этот путь и начал прокладывать Леонард Эйлер.
естественно, и до крайней четверти XVIII века теория Ньютона сталкивалась с трудностями. В этот период встречались простые функции, первообразные которых не могут быть выражены через простые функции. Знали арифметики и некие несобственные интегралы, в том числе и расходящиеся. Но такового рода факты были единичными и установившейся действенной концепции интеграла нарушить не могли. Другим оказалось положение в крайней четверти XVIII и в особенности сначала XIX века.
С 70-х годов XVIII века решение задач аналитической механики, физики и остальных дисциплин потребовало существенное развитие понятия определенного интеграла. Особенное
Это было время, когда величавые идеи Ньютона и Лейбница были размещены сравнимо не так давно и современный математический анализ лишь создавался. Массивные способы, которые принесли с собой эти идеи, находили применение во всех отраслях четкого познания. Применение это шло рука о руку с развитием самого анализа, нередко указывая пути и направления, по которым обязано развиваться новое исчисление. Это была, пожалуй, единственная по собственной интенсивности эра математического творчества, и Эйлер был один из немногих по собственной продуктивности творцов. Его «Введение в анализ нескончаемо малых», «Основания дифференциального исчисления» и «Основания интегрального исчисления» были первыми трактатами, в каких уже широкий, но разрозненный материал новейшего анализа был объединен в цельную науку. В их был выработан тот скелет современного анализа, который сохранился и до нашего времени.
Разработка приемов вычисления двойных и тройных интегралов показала, что вычислять эти интегралы так, как вычисляли обыденный определенный интеграл — с помощью неопределенного, весьма тяжело либо даже нереально. Потому арифметики обязаны были сохранять теорию Ньютона лишь словестно, а на самом деле, при решении задач четких наук, стали на путь Лейбница. Они вычисляли надлежащие интегральные суммы (в прямоугольных, цилиндрических и сферических координатах) и находили их пределы.
Короче говоря, разработка методов вычисления новейших видов определенного интеграла показала, что обычный, двойной и т. д. определенный интегралы должны быть обусловлены сами по для себя независимо от понятия неопределенного интеграла. Но каждое слагаемое хоть какой интегральной суммы является нескончаемо малой величиной. Тем не только лишь ставился вопросец о легализации ранее “изгоняемого” понятия нескончаемо малого, да и о раскрытии его настоящего содержания и о соответственном его использовании. Как уже указывалось, чтоб всё это создать было надо преодолеть — обобщить, развить обычное (Эйлерово) истолкование функции и понятия предела.
В связи с сиим появился вопросец о существовании пределов интегральных сумм, слагаемые которых могли быть нескончаемо малыми. В первой четверти XIX века понятие нескончаемо малой оказалось нужным и для исследования и сравнения параметров непрерывных и разрывных функций. Получение основополагающих результатов соединено тут с именованием Коши. “Меж почти всеми понятиями, — указывал Коши, — тесновато связанными со качествами нескончаемо малых, следует поместить понятие о непрерывности и прерывности функций”. Здесь же Коши дает толкование непрерывности функции, которое наиболее чем ясно подтверждает ясность этого его утверждения.
Новенькая постановка задач обоснования математического анализа ясно демонстрировала, что дело не только лишь в признании и применении нескончаемо малых — это делали и ранее! — но до этого всего в научном толковании их содержания и обоснованном на этом использовании их в методах математического анализа. Но, чтоб это создать было надо преодолеть господствовавшее в XVIII веке узенькое истолкование понятия предела, создать общую теорию пределов.
исследование разрывных функций и сравнение их с функциями непрерывными принудило признать то, что ранее числилось неосуществимым: что предел, к которому стремиться последовательность значений функции, при стремлении аргумента в некой точке может оказаться хорошим от значения функции в данной нам точке. Означает, предел не постоянно является “крайним” значением переменной, но во всех вариантах предел есть число, к которому переменная приближается неограниченно. Как следует, dx и dy не нужно нули либо “мистически” животрепещуще нескончаемо малые; нескончаемо малая — это переменная, имеющая пределом нуль, при этом факт этот с противоречиями и феноменами не связан.
Коши преодолел и вторую ограничительную тенденцию в принятой до него трактовке понятия предела. Он признал, что переменная может приближаться к собственному лимиту не только лишь однообразно, да и колеблясь, иногда принимая значения, равные её лимиту. Это событие придало теории Коши нужную общность и исключительную упругость. Мы до сего времени следуем пути, намеченному Огюстеном Луи Коши, с теми усовершенствованиями, которые были внесены во 2-ой половине XIX века К. Вейерштрассом.
работы Коши и Вейерштрасса окончили создание традиционного математического анализа, Тем подведя результат многолетнего развития интегрального исчисления.
Перечень литературы
Большакова А. А. Три кризиса в развитии арифметики. Дипломная работа; Астрахань: АГПИ, 1996.
Детская энциклопедия для среднего и старшего возраста. Т.2; М.: Просвещение, 1965.
Математическая энциклопедия. Ред. Виноградова. Т.2; М.: Сов. Энциклопедия, 1979.
Фихтенгольц Г.М. Базы математического анализа. Т.1; М.: Наука, 1968.
]]>